
24.(本小题满分10分)
(1)已知实数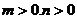 ,求证:
,求证: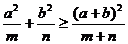 ;
;
(2) 利用(1)的结论,求函数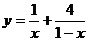 (其中
(其中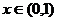 )的最小值.
)的最小值.
吉林市普通中学2009-2010学年度高中毕业班下学期期末教学质量检测
23.(本小题满分10分)
已知直线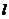 经过点
经过点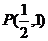 ,倾斜角
,倾斜角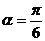 ,圆
,圆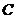 的极坐标方程为
的极坐标方程为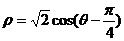
(1)写出直线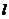 的参数方程,并把圆C的方程化为直角坐标方程;
的参数方程,并把圆C的方程化为直角坐标方程;
(2)设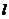 与圆C相交与两点
与圆C相交与两点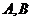 ,求点
,求点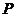 到
到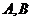 两点的距离之积.
两点的距离之积.
22.(本小题满分10分)
已知:直线AB过圆心O,交⊙O于AB, 直线AF交⊙O于AF(不与B重合),直线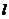 与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连结AC.
与⊙O相切于C,交AB于E,且与AF垂直,垂足为G,连结AC.
求证:(1)∠BAC=∠CAG;
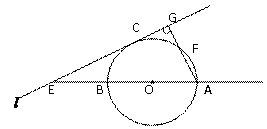
(2) 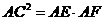 .
.
21.(本小题满分12分)
直线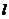 :
: 恒过定点C,
恒过定点C,
以点C为圆心,2为半径作圆C.
(1) 求圆C方程;
(2) 设点C关于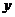 轴的对称点为
轴的对称点为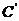 ,动点M在曲线E上,在
,动点M在曲线E上,在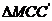 中,满足
中,满足
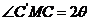 ,
,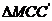 的面积为
的面积为 ,求曲线E的方程;
,求曲线E的方程;
(3)点P在(2)中的曲线E上,过点P作圆C的两条切线,切点为Q、R,
求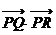 的最小值.
的最小值.
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
20. (本小题满分12分)
已知函数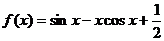 ,
,
(1)求函数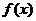 的单调区间;
的单调区间;
(2)不等式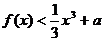 在区间
在区间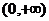 上恒成立,求实数
上恒成立,求实数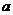 的取值范围.
的取值范围.
19. (本小题满分12分)
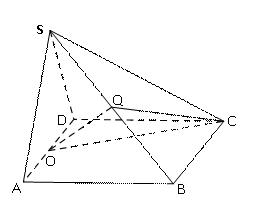 已知四棱锥
已知四棱锥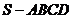 中,
中,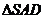 是边长为2的正三角形,平面
是边长为2的正三角形,平面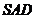
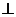 平面
平面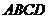 ,四边形
,四边形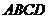 为菱形,
为菱形,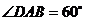 ,O为AD的中点, Q为SB的中点,
,O为AD的中点, Q为SB的中点,
H为OQ的中点
(1)求证:OQ∥平面SCD ;
(2)求二面角D-OC-Q的余弦值;
(3)证明:在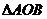 内存在一点M,使
内存在一点M,使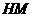
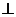 平面
平面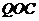 .
.
18. (本小题满分12分)
甲乙两个学校高三年级分别有1100人,1000人,为了统计两个学校在地区二模考试的数学科目成绩,采用分层抽样抽取了105名学生的成绩,并作出了部分频率分布表如下:(规定考试成绩在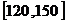 内为优秀)
内为优秀)
甲校:
|
分组 |
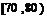 |
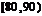 |
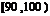 |
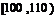 |
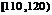 |
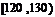 |
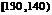 |
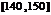 |
|
频数 |
2 |
3 |
10 |
15 |
15 |
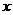 |
3 |
1 |
乙校:
|
分组 |
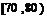 |
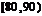 |
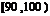 |
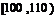 |
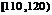 |
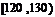 |
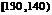 |
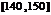 |
|
频数 |
1 |
2 |
9 |
8 |
10 |
10 |
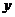 |
3 |
(1)
计算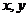 的值,并分别估计两个学校数学成绩的优秀率;
的值,并分别估计两个学校数学成绩的优秀率;
(2)
由以上统计数据填写下面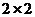 列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
列联表,并判断是否有97.5%的把握认为两个学校的数学成绩有差异.
|
|
甲 校 |
乙 校 |
总 计 |
|
优
秀 |
|
|
|
|
非优秀 |
|
|
|
|
总
计 |
|
|
|
附: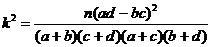
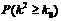 |
0.10 |
0.025 |
0.010 |
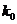 |
2.706 |
5.024 |
6.635 |
17.(本小题满分12分)
已知等差数列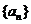 的首项
的首项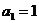 ,公差
,公差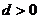 ,等比数列
,等比数列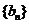 ,满足
,满足
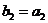 ,
,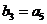 ,
,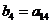 .
.
(1) 求数列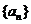 与
与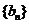 的通项;
的通项;
(2)设数列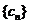 满足
满足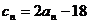 ,求数列
,求数列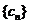 的前
的前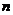 项和
项和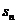 的最小值,
的最小值,
并求出此时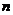 的值.
的值.
16.设函数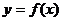 为定义域
为定义域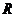 上的奇函数,满足
上的奇函数,满足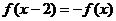 ,对一切
,对一切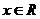
都成立,又知当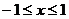 时,
时,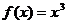 ,则下列四个命题
,则下列四个命题
①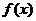 是以
是以 为周期的周期函数;
为周期的周期函数;
②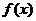 在
在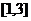 上的解析式
上的解析式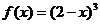 ;
;
③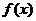 在点
在点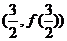 处的切线方程为
处的切线方程为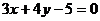 ;
;
④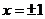 是函数
是函数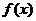 图像的对称轴.
图像的对称轴.
其中正确的是_____________.
三:解答题:解答应写出文字说明,证明过程或演算步骤.
15.如图,给出函数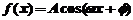
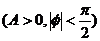
 图像的一部分,则
图像的一部分,则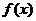 的解析式为
的解析式为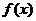 =_________________.
=_________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com