
7.△ABC满足: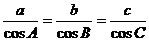 ,那么此三角形的形状是
( )
,那么此三角形的形状是
( )
A.直角三角形 B.正三角形 C.任意三角形 D.等腰三角形
6. 在△ABC中,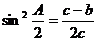 ,则△ABC的形状为 ( )
,则△ABC的形状为 ( )
A .正三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形
5.锐角△ABC中,如果a=1,b=2,那么c的范围是 ( )
A.1<c<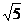 B.
B.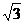 <c<
<c<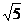 C.
C.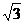 <c<
<c<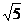 D .1<c<3
D .1<c<3
4.△ABC中,如果lgsinA-lgsinB-lgcosC=lg2,那么有 ( )
A.A=90º B.b=c C.a=b D.a=b=c
3.△ABC中,如果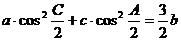 ,那么有
( )
,那么有
( )
A.a+b=2c B.b+c=2a C. a+c=2b D.a=b=c
2.△ABC中,“A>B”是“sinA>sinB”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
1. 在△ABC中,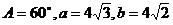 ,则B等于
( )
,则B等于
( )
A .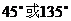 B.
B. 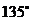 C.
C. 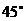 D. 以上都不对
D. 以上都不对
2. 已知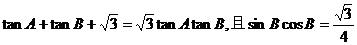 ,
,
则△ABC是 ( )
A .正三角形
B.正三角形或直角三角形
C.直角三角形
D.直角三角形或等腰三角形
题型四 三角函数实际应用
例4.(2007.山东)如图,甲船以每小时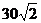 海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于
海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于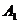 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西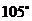 方向的
方向的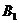 处,此时两船相距20海里,当甲船航行20分钟到达
处,此时两船相距20海里,当甲船航行20分钟到达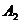 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西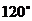 方向的
方向的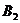 处,此时两船相距
处,此时两船相距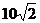 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
跟踪练习:
在海岸A处发现北偏东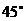 方向,距A 处(
方向,距A 处(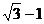 )海里的B处有一艘走私船,在A处北偏西
)海里的B处有一艘走私船,在A处北偏西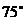 方向,距A处2海里的C处的我方缉私船,奉命以
方向,距A处2海里的C处的我方缉私船,奉命以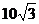 海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度,从B处向北偏东
海里/小时的速度追截走私船,此时走私船正以10海里/小时的速度,从B处向北偏东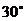 方向逃窜.问:缉私船应沿什么方向行驶才能最快截获走私船?并求出所需时间.
方向逃窜.问:缉私船应沿什么方向行驶才能最快截获走私船?并求出所需时间.
题型一 利用正弦定理求解三角形
典例1.已知下列各三角形中的两边及其一边的对角,先判断三角形是否有解?
有解得做出解答.
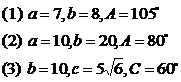
思考:在△ABC中,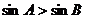 是
是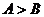 的什么条件?
的什么条件?
题型二 余弦定理应用
典例2.在△ABC中,a、b、c分别是角A、B、C的对边,且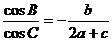 .
.
(1) 求角B的大小;
(2)
若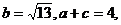 求△ABC的面积.
求△ABC的面积.
跟踪练习:
在在△ABC中,A、B、C所对的边分别为a、b、c,且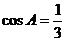
(1) 求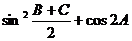 的值
的值
(2) 若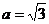 ,求bc的最大值
,求bc的最大值
题型三 判断三角形的形状
例3 、在△ABC中,已知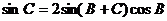 ,那么△ABC一定是 ( )
,那么△ABC一定是 ( )
A .等腰直角三角形
B.等腰三角形
C.直角三角形
D.等边三角形
跟踪练习
1. △ABC中,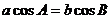 ,则△ABC的形状为
( )
,则△ABC的形状为
( )
A .等腰三角形
B.直角三角形
C.等腰三角形或直角三角形
D.等腰直角三角形
4.三角形常用面积公式:
(1)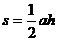
(2)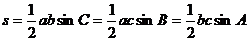
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com