
7. 解析:C
6. 解析:C 根据 线线、线面、面面位置关系,易知①④为真命题,选C.
线线、线面、面面位置关系,易知①④为真命题,选C.
5. 解析:C  ,
,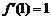 ,
,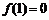 .
.
切线方程为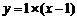 ,即
,即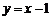 ,选C.
,选C.
4. 解析:B 由三视图知该几何体是直三棱柱,底面是直角三角形,且直角边分别为3,4.
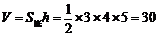 .
.
3. 解析:D 命题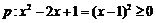
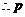 为假命题.
为假命题.
命题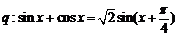 . 当
. 当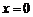 时,
时, ,
,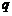 为真命题,故选D.
为真命题,故选D.
2. 解析:C 易知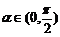 ,
,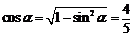 ,
,
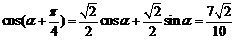 .
.
1. 解析:A  ,
,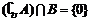 .
.
21.若数列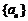 满足
满足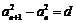 ,其中
,其中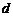 为常数,则称数列
为常数,则称数列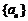 为等方差数列.已知等方差数列
为等方差数列.已知等方差数列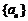 满足
满足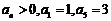 .
.
(1)求数列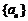 的通项公式;
的通项公式;
(2)求数列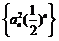 的前
的前 项和;
项和;
(3)记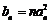 ,则当实数
,则当实数 大于4时,不等式
大于4时,不等式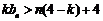 能否对于一切的
能否对于一切的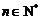 恒成立?请说明理由.
恒成立?请说明理由.
湖南省长沙市一中高三第九次月考答案
文科数学
20. 已知点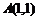 是椭圆
是椭圆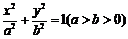 上的一点,
上的一点, 是椭圆的两个焦点,且满足
是椭圆的两个焦点,且满足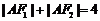 .
.
(1)求椭圆的方程及离心率;
(2)设点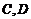 是椭圆上的两点,直线
是椭圆上的两点,直线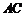 、
、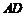 的倾斜角互补,试判断直线
的倾斜角互补,试判断直线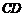 的斜率是否为定值?并说明理由.
的斜率是否为定值?并说明理由.
19.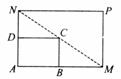 如图所示,将一矩形花坛
如图所示,将一矩形花坛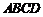 扩建成一个更大的矩形花园
扩建成一个更大的矩形花园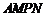 ,要求
,要求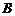 在
在 上,
上,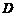 在
在 上,且对角线
上,且对角线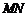 过
过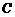 点,
点,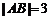 米,
米,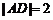 米.
米.
(1)要使矩形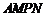 的面积大于32平方米,则
的面积大于32平方米,则 的长应在什么范围内?
的长应在什么范围内?
(2)当 、
、 的长度是多少时,矩形
的长度是多少时,矩形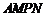 的面积最小?并求出最小面积.
的面积最小?并求出最小面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com