
2.若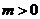 ,则
,则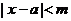 且
且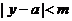 是
是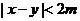 的 ( )
的 ( )
 充分不必要条件
充分不必要条件  必要不充分条件
必要不充分条件
 充要条件
充要条件
 既不充分也不必要条件
既不充分也不必要条件
1.若 ,且
,且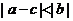 ,则
( )
,则
( )
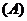
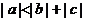


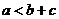
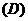
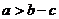
例1.已知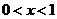 ,
,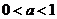 ,试比较
,试比较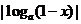 和
和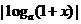 的大小.
的大小.
例2.求证: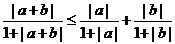 .
.
例3.设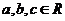 ,已知二次函数
,已知二次函数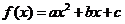 ,
,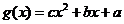 ,且当
,且当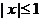 时,
时, ,(1)求证:
,(1)求证: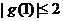 ;(2)求证:
;(2)求证: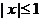 时,
时, .
.
例4.设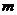 等于
等于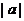 、
、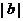 和
和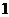 中最大的一个,当
中最大的一个,当 时,求证:
时,求证: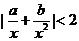 .
.
5.设有两个命题:①不等式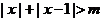 的解集是
的解集是 ;②函数
;②函数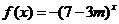 是减函数,如果这两个命题中有且只有一个是真命题,则实数
是减函数,如果这两个命题中有且只有一个是真命题,则实数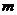 的取值范围是
.
的取值范围是
.
4.已知集合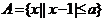 ,
, ,且
,且 ,则
,则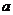 的取值范围是
.
的取值范围是
.
3.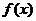 为
为 上的增函数,
上的增函数,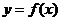 的图象过点
的图象过点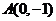 和下面哪一点时,能确定不等式
和下面哪一点时,能确定不等式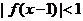 的解集为
的解集为 ( )
( )
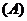
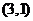

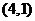
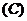
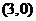
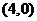
2.不等式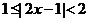 的解集为
( )
的解集为
( )
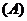
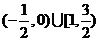

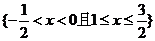
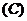

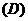
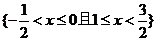
1.不等式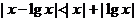 的解集为 ( )
的解集为 ( )




2.绝对值不等式的解法:
① 时,
时,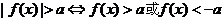 ;
;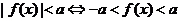 ;
;
②去绝对值符号是解绝对值不等式的常用方法;
③根据绝对值的几何意义,通过数形结合解绝对值不等式.
1.含绝对值的不等式的性质:
①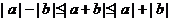 ,当 时,左边等号成立;当
,当 时,左边等号成立;当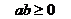 时,右边等号成立.②
时,右边等号成立.②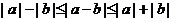 ,当 时,左边等号成立;当 时,右边等号成立.③进而可得:
,当 时,左边等号成立;当 时,右边等号成立.③进而可得: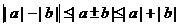 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com