
22、已知数列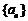 满足
满足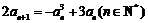 且
且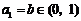
(1) 证明: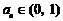 ;
;
(2) 比较an与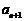 的大小;
的大小;
(3) 是否存在正实数c,使得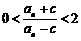 ,对一切
,对一切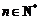 恒成立?若存在,则求出c的取值范围;若不存在,说明理由.
恒成立?若存在,则求出c的取值范围;若不存在,说明理由.
河南鹤壁中学09-10学年高二下学期第一次考试
21、设函数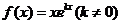
(Ⅰ)求曲线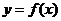 在点
在点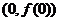 处的切线方程;
处的切线方程;
(Ⅱ)求函数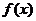 的单调区间;
的单调区间;
(Ⅲ)若函数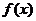 在区间
在区间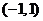 内单调递增,求
内单调递增,求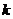 的取值范围.
的取值范围.
20.(本小题满分12分)已知A(1,f′(1))是函数y=f(x)的导函数图像上的一点,点B的坐标为(x,㏑(x+1)),向量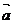 =(1,1),设f(x)=
=(1,1),设f(x)=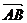 ·
·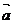
(1)求函数y=f(x)的表达式;
(2)若x∈[-1,1]时,不等式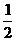 x
x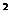 ≤f(x
≤f(x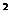 )+m
)+m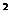 -
-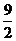 m-3都恒成立,求实数m 的取值范围.
m-3都恒成立,求实数m 的取值范围.
19、(本小题满分12分)用数学归纳法证明:
18、(本小题满分12分)设两抛物线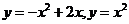 所围成的图形为
所围成的图形为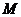 ,求
,求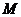 的面积.
的面积.
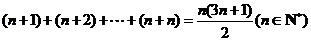
17、(本小题满分10分)四个不同的小球放入编号为1、2、3、4四个盒子中,依下列条件各有多少种放法。
(1)每个盒子各放一个;
(2)四个盒子恰有一个空着.
16、对正整数n,设曲线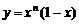 在x=2处的切线与y轴交点的纵坐标为
在x=2处的切线与y轴交点的纵坐标为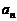 ,则数列
,则数列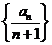 的前n项和等于 .
的前n项和等于 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com