
20. (本小题满分12分)
(本小题满分12分)
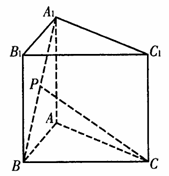
已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为
A1B上的点,且PC⊥AB.
(Ⅰ)求二面角P-AC-B的正切值;
(Ⅱ)求点B到平面PAC的距离.
21 (本小题满分12分)
已知定义在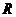 上的函数
上的函数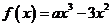 (
(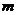 为常数)。
为常数)。
(1)
若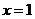 是函数
是函数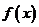 的一个极值点,求实数
的一个极值点,求实数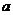 的值;
的值;
(2)
若函数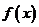 在
在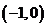 上是增函数,求实数
上是增函数,求实数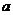 的取值范围;
的取值范围;
(3)
若函数 在
在 处取得最大值,求正数
处取得最大值,求正数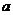 的取值 范围。
的取值 范围。
22(本小题满分12分)
已知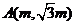 k*s#5^u和
k*s#5^u和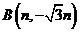
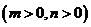 两点分别在射线
两点分别在射线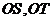 上移动,且
上移动,且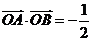 (
(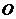 为坐标原点),动点
为坐标原点),动点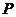 满足
满足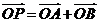
(1)
求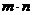 的值
的值
(2)
求点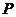 的轨迹
的轨迹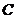 的方程,并说明它表示怎样的曲线?
的方程,并说明它表示怎样的曲线?
(3)
若直线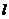 过点
过点 交(2)中曲线
交(2)中曲线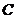 于
于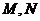 两点,且
两点,且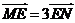 ,求
,求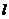 的方程.
的方程.
19. (本小题满分12分)
甲、乙两支中学生足球队,苦战90分钟,比分2:2,现决定各派5名队员,每人射一个点球决定胜负,假设两支球队派出的队员点球命中概率均为0.5。
(1)两队球员一个间隔一个出场射球,有多少种不同的出场顺序?
(2)不考虑乙球队,甲球队五名队员有连续两个队员射中,且其余队员均未射中,概率是多少?
(3)甲乙两队各射完5个点球后,再次出现平局的概率是多少?
18. (本小题满分12分)
设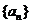 是等差数列,
是等差数列,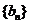 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 ,
,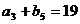 ,
, .
.
(1)求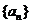 k*s#5^u和
k*s#5^u和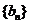 的通项公式; (2)求数列
的通项公式; (2)求数列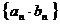 的前n项k*s#5^u和
的前n项k*s#5^u和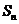 .
.
17. (本小题满分10分)
已知函数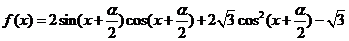 ,
,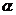 为常数.
为常数.
(Ⅰ)求函数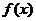 的周期;
的周期;
(Ⅱ)若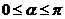 时,求使函数
时,求使函数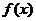 偶函数的
偶函数的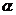 值.
值.
16. 点P、A、B、C在一个表面积为12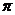 的球面上,三棱锥P-ABC中,E、F分别是AC、AB的中点,△ABC、△PEF都是正三角形,PF⊥AB,则△ABC的边长为
.
的球面上,三棱锥P-ABC中,E、F分别是AC、AB的中点,△ABC、△PEF都是正三角形,PF⊥AB,则△ABC的边长为
.
15. 抛物线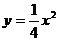 上的一点M到其焦点的距离为5,则点M的纵坐标是
;
上的一点M到其焦点的距离为5,则点M的纵坐标是
;
14. 已知数列1, a1,
a2, 4成等差数列,1, b1, b2,
b3, 4成等比数列,则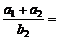 _______.
_______.
13.
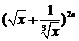 展开式的第6项系数最大,则其常数项为_______.
展开式的第6项系数最大,则其常数项为_______.
12. 在正四面体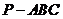 中,D、E、F分别是AB、BC、CA的中点,下面四个结论中不成立的是( )
中,D、E、F分别是AB、BC、CA的中点,下面四个结论中不成立的是( )
A.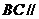 平面
平面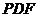 B.
B.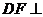 平面
平面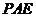
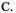 平面
平面 平面
平面 D.平面
D.平面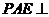 平面
平面
第II卷(非选择题 共90分)
11. 设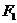 、
、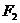 为曲线
为曲线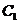 :
: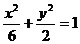 的焦点,P是曲线
的焦点,P是曲线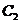 :
: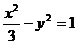 与
与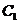 的一个交点,则
的一个交点,则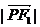 ·
·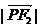 的值为( )
的值为( )
A.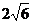 B.
B.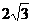
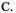 4
D.3
4
D.3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com