
22.(本小题满分14分)
已知抛物线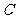 :
: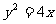 的准线与
的准线与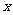 轴交于
轴交于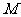 点,过
点,过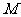 点斜率为
点斜率为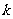 的直线
的直线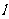 与抛物线
与抛物线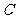 交于
交于 、
、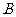 两点(
两点( 在
在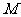 、
、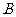 之间).
之间).
(1)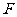 为抛物线
为抛物线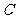 的焦点,若
的焦点,若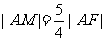 ,求
,求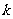 的值;
的值;
(2)如果抛物线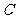 上总存在点
上总存在点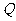 ,使得
,使得 ,试求
,试求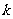 的取值范围.
的取值范围.
贵州省云峰中学2010届高三下学期3月月考
21.(本小题满分12分)已知椭圆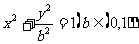 的左焦点为
的左焦点为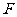 ,左右顶点分别为
,左右顶点分别为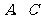 ,上顶点为
,上顶点为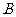 ,过
,过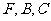 三点作圆
三点作圆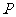 ,其中圆心
,其中圆心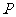 的坐标为
的坐标为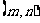
(1)当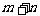 >
>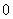 时,椭圆的离心率的取值范围
时,椭圆的离心率的取值范围
(2)直线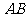 能否和圆
能否和圆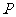 相切?证明你的结论
相切?证明你的结论
20.(本小题满分12分)各项均为正数的数列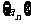 中,
中,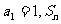 是数列
是数列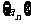 的前
的前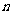 项和,对任意
项和,对任意 ,有
,有
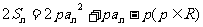
(1)求常数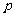 的值;
的值;
(2)求数列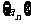 的通项公式;
的通项公式;
(3)记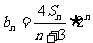 ,求数列
,求数列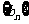 的前
的前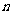 项和
项和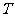 。
。
18.(本小题满分12分)甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设每人面试合格的概率都是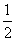 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(Ⅰ)至少有1人面试合格的概率;
(Ⅱ)签约人数 的分布列和数学期望.
的分布列和数学期望.
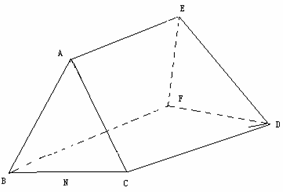 19.(本小题满分12分)多面体
19.(本小题满分12分)多面体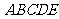 中,
中,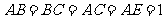 ,
,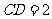 ,
,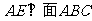 ,
,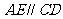 。
。
(1)求证: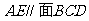 ;
;
(2)求证: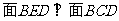 。
。
17.(本小题满分12分)
已知△ABC的面积S满足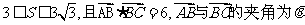
(1)求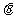 的取值范围;
的取值范围;
(2)求函数 的最大值
的最大值




16.观察下列等式:

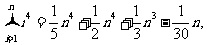
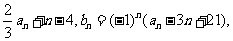
……………………………………
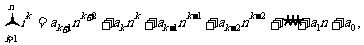
可以推测,当x≥2(k∈N*)时,
ak-2= .
15.对有n(n≥4)个元素的总体{1,2,3,…,n}进行抽样,先将总体分成两个子总体
{1,2,…,m}和{m+1、m+2,…,n}(m是给定的正整数,且2≤m≤n-2),再从每个子总体中各随机抽取2个元素组成样本,用Pij表示元素i和f同时出现在样本中的概率,则P1m= ;所有Pif(1≤i<j≤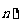 的和等于 .
的和等于 .
14.若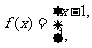
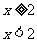 ,
, ,则方程
,则方程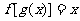 的解为 .
的解为 .
13.在某项测量中,测量结果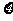 服从正态分布
服从正态分布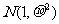 .若
.若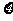 在
在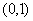 内取值的概率为0.4,则
内取值的概率为0.4,则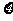 在
在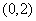 内取值的概率为
.
内取值的概率为
.
12.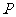 是椭圆
是椭圆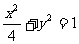 上的一点,
上的一点,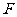 为一个焦点,且
为一个焦点,且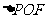 为等腰三角形(
为等腰三角形(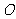 为原点),则点
为原点),则点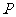 的个数为( )
的个数为( )
A. 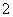 B.
B. 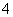 C.
C. 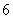 D.
D. 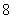
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com