
5、(理)将函数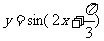 的图像经怎样平移后所得的图像关于点
的图像经怎样平移后所得的图像关于点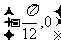 中心对称( ).
中心对称( ).
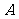 向左移
向左移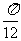
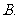 向左移
向左移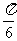
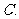 向右移
向右移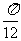
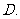 向右移
向右移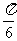
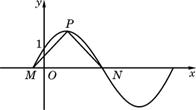
(文) 如右图所示,点P是函数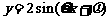 (x∈R,
(x∈R, )的图像的最高点,M、N是图像与
)的图像的最高点,M、N是图像与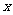 轴的交点,
若
轴的交点,
若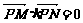 ,则
,则
A.8 B.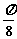 C.
C.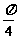 D.
D.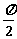
4.已知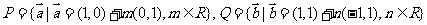 是两个向量集合,则
是两个向量集合,则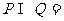 ( )
( )
A.{(1,1)} B.{(-1,1)} C.{(1,0)} D.{(0,1)}
3. 条件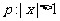 ,条件
,条件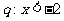 ,则
,则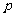 是
是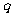 的( )
的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
2.已知直线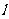 过点
过点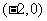 ,当直线
,当直线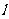 与圆
与圆 有两个交点时,其斜率
有两个交点时,其斜率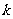 的取值范围是( )
的取值范围是( )
A.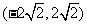 B.
B.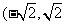 ) C.
) C.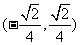 D.
D.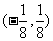
1.(理)设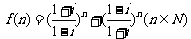 ,则集合
,则集合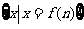 中元素的个数为( )
中元素的个数为( )
A.1 B.2 C.3 D.无穷多个
(文)复数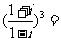 ( )A. l B.-1 C.i D.-i
( )A. l B.-1 C.i D.-i
22.(本小题满分12分)
设A(x1,y1),B(x2,y2)是椭圆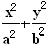 =1(a>b>0)上的两点,已知向量m(
=1(a>b>0)上的两点,已知向量m(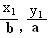 )
,n(
)
,n(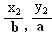 ),若m·n=0且椭圆的离心率e=
),若m·n=0且椭圆的离心率e=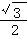 ,短轴长为2,O为坐标原点:
,短轴长为2,O为坐标原点:
(Ⅰ)求椭圆的方程:
(Ⅱ)若直线AB过椭圆的焦点F(0,c),(为半焦距),求直线AB的斜k率的值:
(Ⅲ)试问:△AOB的面积是否为定值?如果是,请给予证明:如果不是,请说明理由。
21. (本小题满分12分)
设函数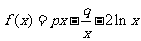 ,且
,且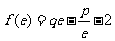 (
(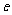 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求实数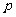 与
与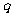 的关系;
的关系;
(Ⅱ)若函数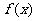 在其定义域内为单调函数,求实数
在其定义域内为单调函数,求实数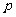 的取值范围;
的取值范围;
(Ⅲ)设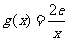 ,若存在
,若存在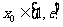 ,使得
,使得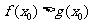 成立,求实数
成立,求实数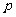 的取值范围.
的取值范围.
20. (本小题满分12分)
已知抛物线C: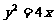 ,过点A(-1,0)的直线交抛物线C于P、Q两点,设
,过点A(-1,0)的直线交抛物线C于P、Q两点,设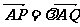 .
.
(Ⅰ)若点P关于x轴的对称点为M,求证:直线MQ经过抛物线C的焦点F;
(Ⅱ)若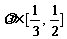 ,求当
,求当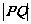 最大时,直线PQ的方程.
最大时,直线PQ的方程.
19.(本小题满分12分)某隧道长2150米,通过隧道的车速不能超过20米/秒.一个由55辆车身都为10米的同一车型组成的运输车队匀速通过该隧道.设车队的速度为x米/秒,根据安全和车流的需要,相邻两车均保持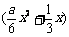 米的距离,其中a为常数且
米的距离,其中a为常数且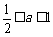 ,自第一辆车车头进入隧道至第55辆车车尾离开隧道所用时间为y(秒) .
,自第一辆车车头进入隧道至第55辆车车尾离开隧道所用时间为y(秒) .
(1)将y表示为x的函数;
(2)求车队通过隧道所用时间取最小值时车队的速度.
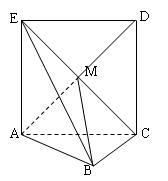
18、(本小题满分12分)如图,正方形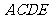 所在的平面与平面
所在的平面与平面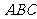 垂直,
垂直,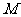 是
是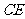 和
和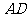 的交点,
的交点,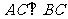 ,且
,且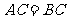 .
.
(1)求证: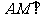 平面
平面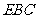 ;
;
(2)求直线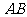 与平面
与平面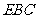 所成的角的大小;
所成的角的大小;
(3)求二面角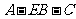 的大小.
的大小.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com