
5.函数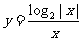 的大致图象是 ( )
的大致图象是 ( )
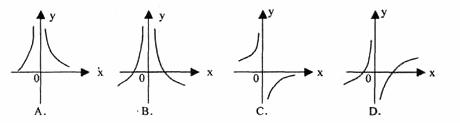
4.在空间中,有如下命题:①互相平行的两条直线在同一平面内的射影必然是互相平行的两条直线;②若平面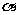 内任意一条直线都平行平面
内任意一条直线都平行平面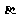 ,则平面
,则平面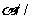 平面
平面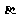 ;③若平面
;③若平面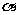 与平面
与平面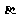 的交线为m,平面
的交线为m,平面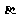 内的直线
内的直线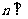 直线m,则直线
直线m,则直线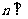 平面
平面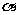 ;④若平面
;④若平面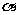 内有两条相交直线和平面
内有两条相交直线和平面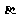 内一条直线
内一条直线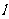 垂直,则
垂直,则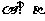 ,其中正确命题的个数为( )
,其中正确命题的个数为( )
A.1个 B.2个 C.3个 D.4个
3.某中学开学后从高一年级的学生中随机抽取90名学生进行家庭情况调查。经过一段时间后再次从这个年级随机抽取100名学生进行学情调查,发现有20名同学上次被抽到过,估计这个学校高一年级的学生人数为 ( )
A.180 B.400 C.450 D.2000
2.条件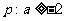 ;条件
;条件
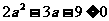 ,则
,则 的 ( )
的 ( )
A.充分非必要条件 B.必要非充分条件
C.充分必要条件 D.既非充分也非必要条件
1.集合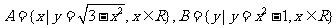 ,则A∩B= ( )
,则A∩B= ( )
A. B.
B.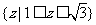
C. D.
D.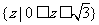
21.(本题满分14分)
设函数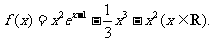
(I)求函数的单调区间;
(II)求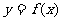 在[0,
在[0,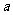 ]
]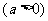 上的最小值;
上的最小值;
(III)当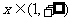 时,证明:对任意
时,证明:对任意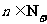
安徽省宿州市2010年高三第三次教学质量检测
20、(本小题满分13分)
对于给定数列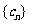 ,如果存在实常数
,如果存在实常数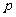 、
、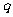 ,使得
,使得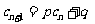 对于任意
对于任意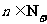 都成立,我们称数列
都成立,我们称数列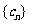 是 “线性数列”.
是 “线性数列”.
(I)如果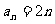 ,
,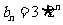 ,
,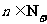 ,那么数列
,那么数列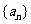 、
、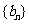 是否为“线性数列”?
是否为“线性数列”?
若是,分别指出它们对应的实常数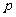 、
、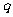 ;若不是,请说明理由;
;若不是,请说明理由;
(II)若数列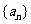 满足
满足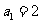 ,
,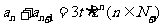 ,
,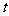 为常数.
为常数.
① 求数列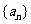 前
前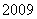 项的和;
项的和;
② 是否存在实数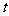 ,使数列
,使数列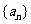 是“线性数列”,如果存在,求出所有
是“线性数列”,如果存在,求出所有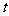 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
19、(本小题满分12分)
已知抛物线C: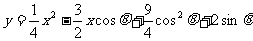
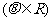
(I)当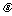 变化时,求抛物线C的顶点的轨迹E的方程;
变化时,求抛物线C的顶点的轨迹E的方程;
(II)已知直线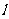 过圆
过圆 的圆心
的圆心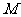 ,交(I)中轨迹E于A、B两点,若
,交(I)中轨迹E于A、B两点,若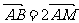 ,求直线
,求直线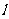 的方程.
的方程.
18、(本小题满分12分)
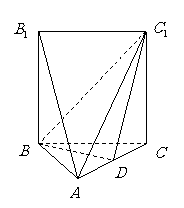 如图,五面体
如图,五面体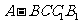 中,
中,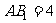 .底面
.底面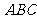 是正三角形,
是正三角形,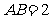 .四边形
.四边形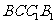 是矩形,平面
是矩形,平面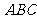
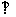 平面
平面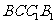
(I)求这个几何体的体积;
(Ⅱ)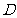 在
在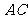 上运动,问:当
上运动,问:当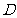 在何处时,有
在何处时,有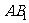 ∥平面
∥平面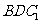 ,请说明理由;
,请说明理由;
(III)求二面角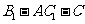 的余弦值.
的余弦值.
17、(本小题满分12分)
宿州市教育局举行科普知识竞赛,参赛选手过第一关需要回答三个问题,其中前两个问题回答正确各得10分,第三个问题回答正确得20分,若回答错误均得0分,总分不少于30分为过关。如果某位选手回答前两个问题正确的概率都是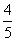 ,回答第三个问题正确的概率是
,回答第三个问题正确的概率是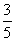 ,且各题回答正确与否互不影响,记这位选手回答这三个问题的总得分为X.
,且各题回答正确与否互不影响,记这位选手回答这三个问题的总得分为X.
(I)求这位选手能过第一关的概率;
(Ⅱ)求X的分布列及数学期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com