4．如图所示，将两个底面平整、干净的铅柱紧压后，两个铅柱就会结合在一起，

　 即使在下面挂一个较重的物体也不会将它们拉开。这个实验表明

　 A．分子间存在斥力　　　　　　　　 B．分子间存在引力

　 C．分子问有间隙　　　　　　　　　 D．分子在永不停息地运动

3．物理知识渗透于我们的生活，以下警示语中与惯性知识无关的是

　 A．汽车后窗贴有“保持车距”　　 B．公路旁立有“雨天路滑，减速慢行”

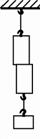　 C．公共场所标有“禁止吸烟”　　 D．交通规则写有“行车时系好安全带”

2．小红在路上骑自行车，若说她是静止的，则选择的参照物可能是

　 A．迎面走来的行人　　　　　　　 B．路旁的树木

　 C．小红骑的自行车　　　　　　　 D．从身边超越的汽车

1．2008年北京奥运会，我国射箭运动员张娟娟获得女子个人金牌，打破了韩国运动员对该项目的垄断．她射箭用的弓上的弦，选用的材料具有良好的

　 A．弹性　　　　　　 B．导热性　　　　 C．磁性　　　　　 D．导电性

20. (本小题满分14分)

设函数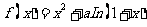有两个极值点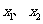，且

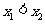
(I)求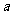的取值范围，并讨论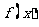的单调性；

(II)证明：　　　　　　

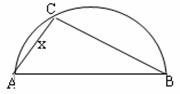
19.(本小题满分14分)如图，两县城A和B相距20km，现计划在两县城外以AB为直径的半圆弧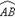上选择一点C建造垃圾处理厂，其对城市的影响度与所选地点到城市的的距离有关，对城A和城B的总影响度为城A与城B的影响度之和，记C点到城A的距离为 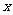km，建在C处的垃圾处理厂对城A和城B的总影响度为,统计调查表明：垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比，比例系数为4；对城B的影响度与所选地点到城B的距离的平方成反比，比例系数为k ,当垃圾处理厂建在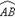的中点时，对城A和城B的总影响度为0.065.

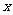(I)将表示成的函数；

(II)讨论(1)中函数的单调性，并判断弧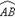上是否存在一点，使建在此处的垃圾处理厂对城A和城B的总影响度最小？若存在，求出该点到城A的距离;若不存在，说明理由。

18．(本小题满分14分)已知椭圆的左右焦点分别为F₁、F₂，点P在椭圆C上，且PF₁⊥F₁F₂, |PF₁|=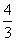,　 |PF₂|=.　

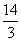(I)求椭圆C的方程；

(II)若直线L过圆的圆心M交椭圆于A、B两点，且A、B关于点M对称，求直线L的方程。

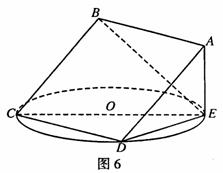
17．(本小题满分14分)

　　 如图6，正方形ABCD所在平面与圆O所在平面相交于CD，线段CD为圆O的弦，AE垂直于圆O所在平面，垂足E是圆O上异于C、D的点，AE＝3，圆O的直径为9．

　　 (1)求证：平面 ABCD ⊥平面 ADE；

　　 (2)求二面角D-BC-E的平面角的正切值．

16．(本小题满分12分)

某公司为庆祝元旦举办了一次抽奖活动，现场准备的抽奖箱里放置了分别标有数字1000、800、600、0的四个球(球的大小相同)．参与者随机从抽奖箱里摸取一球(取后即放回)，公司即赠送与此球上所标数字等额的奖金(元)，并规定摸到标有数字0的球时可以再摸一次，但是所得奖金减半(若再摸到标有数字0的球就没有第三次摸球机会)，求一个参与抽奖活动的人可得奖金的期望值是多少元．

15．(本小题满分12分)

某公司近年来科研费用支出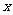万元与公司所获得利润万元之间有如下的统计数据：

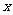	2	3	4	5
	18	27	32	35

(1)请画出上表数据的散点图;

(2)请根据上表提供的数据,用最小二乘法求出关于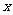的线性回归方程；

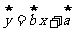(3)试根据(2)求出的线性回归方程,预测该公司科研费用支出为10万元时公司所获得的利润.

参考公式: