
8.曲线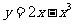 过点(1,1)处的切线方程为
.
过点(1,1)处的切线方程为
.
7.设函数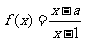 ,集合M=
,集合M=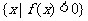 ,P=
,P=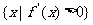 ,若M
,若M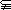 P,则实数a的取值范围是 ( )
P,则实数a的取值范围是 ( )
A.(-∞,1) B.(0,1) C.(1,+∞) D. [1,+∞)
6. 设y=-tanx,则y′= ( )
A.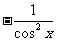 B.
B.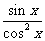 C.
C.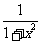 D.-
D.-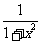
5.曲线y=4x-x2上有两点A(4,0),B(2,4),若曲线上一点P处的切线恰好平行于弦AB,则点P的坐标是 ( )
A.(3,3) B.(1,3) C.(6,-12) D.(2,4)
4.函数y=(2x2-1)2的导数是 ( )
A.16x3-4x2 B.4x3-8x C.16x3-8x D.16x3-4x
3.
下列函数中,导数不等于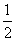 sin2x的是 ( )
sin2x的是 ( )
A.2-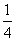 cos2x B.2+
cos2x B.2+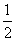 sin2x C.
sin2x C.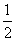 sin2x D.x-
sin2x D.x-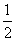 cos2x
cos2x
2. 若f′(x)=x,则[xf(x)]′等于 ( )
A.xf(x)+x B.f(x)+x2 C.x2 D.f(x)
1.
已知f(x)=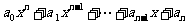 其中n是正整数,则f′(0)等于( )
其中n是正整数,则f′(0)等于( )
A.a0n! B.a0 C.an-1 D.0
2. 复合函数的求导法则 形如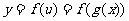 的函数称为复合函数.
的函数称为复合函数.
复合函数求导步骤:分解--求导--回代. 法则:y'|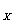 = ·
= ·
☆ 案例分析:
例1. ①[(3x2+1)(4x2-3)]′=( )(4x2-3)+(3x2+1)( ).
②利用导数的定义求函数y=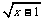 的导数.
的导数.
③设函数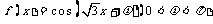 。若
。若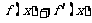 是奇函数,求
是奇函数,求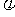 。
。
例2. 求所给函数的导数:
①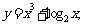 ②
②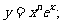 ③
③ 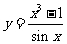 ④y=
④y=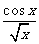 ⑤
⑤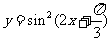 .
.
例3. 设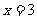 是函数
是函数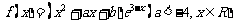 的一个极值点.求
的一个极值点.求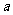 与
与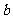 的关系
的关系
式(用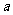 表示
表示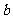 ),并求
),并求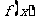 的单调区间.
的单调区间.
例4.已知函数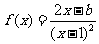 ,求导函数
,求导函数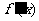 ,并确定
,并确定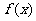 的单调区间.
的单调区间.
例5.已知函数 的图象过点(-1,-6),且函数
的图象过点(-1,-6),且函数
的图象关于y轴对称.
(Ⅰ)求m、n的值及函数y=f(x)的单调区间;
(Ⅱ)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
一轮复习练习 §8.2.导数的运算 姓名
1.两个函数的和、差、积的求导法则
和差的求导法则:(
即:两个函数的和(或差)的导数,等于这两个函数的 (或 ).
积的求导法则:
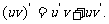 即:两个函数的积的导数,
即:两个函数的积的导数,
等于 的导数乘以 , 加上 乘以 ;
商求导法则:, 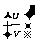 =
=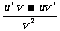 (v
(v 0)即:两个函数的
0)即:两个函数的
等于 的导数乘以 , 减去 乘以 ,再除以分母的平方.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com