
3.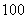 件产品中有
件产品中有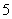 件次品,从中连续取两次,(1)取后不放回,(2)取后放回,则两次都取合格品的概率分别是
件次品,从中连续取两次,(1)取后不放回,(2)取后放回,则两次都取合格品的概率分别是 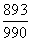 、
、 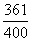 .
.
2.某射手射击一次,击中目标的概率是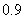 ,他连续射击
,他连续射击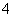 次,且各次射击是否击中目标相互之间没有影响,有下列结论:
次,且各次射击是否击中目标相互之间没有影响,有下列结论:
①他第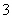 次击中目标的概率是
次击中目标的概率是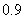 ;②他恰好击中目标
;②他恰好击中目标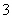 次的概率是
次的概率是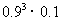 ;
;
③他至少击中目标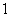 次的概率是
次的概率是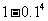 ,其中正确结论的序号 ①③ .
,其中正确结论的序号 ①③ .
1.下列各对事件
(1)运动员甲射击一次,“射中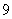 环”与“射中
环”与“射中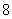 环”,
环”,
(2)甲、乙二运动员各射击一次, “甲射中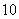 环”与“乙射中
环”与“乙射中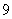 环”,
环”,
(3)甲、乙二运动员各射击一次, “甲、乙都射中目标”与,“甲、乙都没有射中目标”,
(4)甲、乙二运动员各射击一次, “至少有一人射中目标”与,“甲射中目标但乙没有射中目标”,是互斥事件的有 (1),(3) .相互独立事件的有 (2) .
3.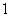 次试验中某事件发生的概率是
次试验中某事件发生的概率是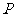 ,则
,则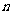 次独立重复试验中恰好发生
次独立重复试验中恰好发生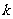 次的概率是 .
次的概率是 .
2.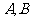 是相互独立事件,则
是相互独立事件,则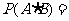 .
.
1.相互独立事件的概念: .
2.会计算事件在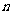 次独立重复试验中恰好发生
次独立重复试验中恰好发生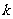 次的概率.
次的概率.
1.了解相互独立事件的意义,会求相互独立事件同时发生的概率;
(四)巩固练习:
1.化简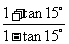 等于 (
等于 ( 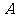 )
)
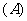
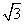
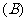
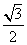
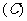
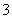
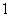
2.已知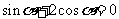 ,则
,则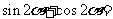
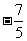 .
.
3.在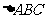 中,
中,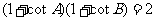 ,则
,则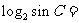
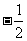 .
.
(三)例题分析:
例1.已知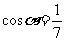 ,
,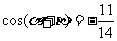 ,
,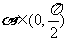 ,
,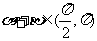 求
求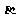 的值.
的值.
解:∵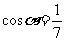 ,
,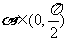 ,∴
,∴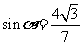 ,
,
又∵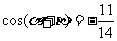 ,
,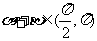 ,∴
,∴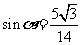 ,
,
∵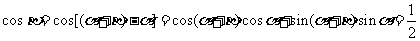 ,
,
又∵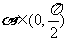 ,
,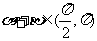 ,
,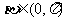 ∴
∴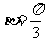 .
.
例2.已知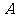 为一三角形的內角,求
为一三角形的內角,求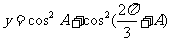 的取值范围.
的取值范围.
解: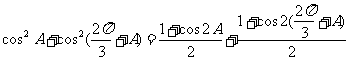
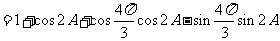
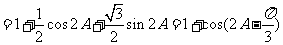 .
.
∵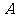 为一三角形內角,
为一三角形內角,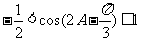 ,
,
∴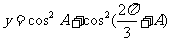 的取值范围是
的取值范围是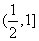 .
.
例3.求值: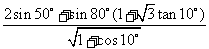 .
.
解:原式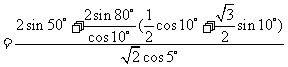
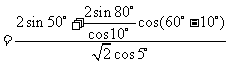
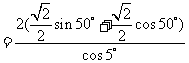
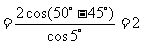 .
.
例4.是否存在两个锐角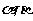 满足(1)
满足(1)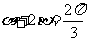 ;(2)
;(2)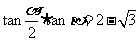 同时成立,若存在,求出
同时成立,若存在,求出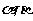 的值;若不存在,说明理由.
的值;若不存在,说明理由.
解:由(1)得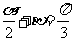 ,∴
,∴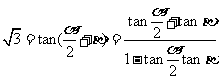 ,
,
∴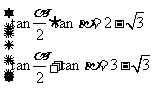 ,∴
,∴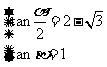 或
或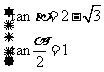 (∵
(∵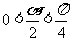 ,∴
,∴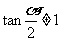 ,舍去),
,舍去),
∴ 为所求满足条件的两个锐角.
为所求满足条件的两个锐角.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com