
22、(本小题满分12分)
已知椭圆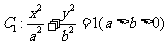 的左、右焦点分别为
的左、右焦点分别为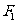 、
、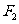 ,其中
,其中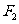 也是抛物线
也是抛物线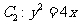 的焦点,
的焦点,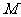 是
是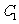 与
与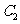 在第一象限的交点,且
在第一象限的交点,且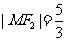 。
。
(Ⅰ)求椭圆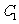 的方程;
的方程;
(Ⅱ)已知菱形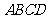 的顶点
的顶点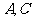 在椭圆
在椭圆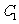 上,对角线
上,对角线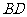 所在的直线的斜率为1.
所在的直线的斜率为1.
① 当直线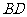 过点
过点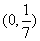 时,求直线
时,求直线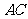 的方程;
的方程;
② 当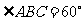 时,求菱形
时,求菱形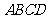 面积的最大值。
面积的最大值。
21、(本小题满分12分)
已知向量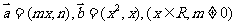 ,令
,令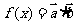 ,其图象在点
,其图象在点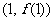 处的切线与直线
处的切线与直线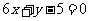 平行,导函数
平行,导函数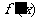 的最小值为
的最小值为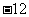 .
.
(Ⅰ)求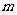 ,
,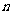 的值;
的值;
(Ⅱ)求函数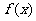 的单调递增区间,并求函数
的单调递增区间,并求函数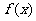 在
在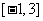 上的最大值和最小值。
上的最大值和最小值。
20、(本小题满分12分)
甲、乙两人各射击一次,击中目标的概率分别是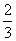 和
和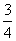 。假设两人射击是否击中目标相互之间没有影响;每人各次射击是否击中目标相互之间也没有影响。
。假设两人射击是否击中目标相互之间没有影响;每人各次射击是否击中目标相互之间也没有影响。
(Ⅰ) 求甲射击4次,至少有1次未击中目标的概率;
(Ⅱ) 求两人各射击4次,甲恰好击中目标2次,且乙恰好击中目标3次的概率;
(Ⅲ) 假设某人连续2次未击中目标,则终止其射击,问乙恰好射击5次后被终止射击的概率是多少?
19、(本小题满分12分)已知直四棱柱ABCD-A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1 的中点,M为线段AC1的中点。
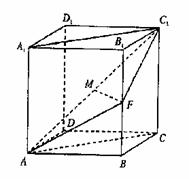 (Ⅰ)求证:直线MF∥平面ABCD;
(Ⅰ)求证:直线MF∥平面ABCD;
(Ⅱ)求证:平面AFC1⊥平面ACC1A1;
(Ⅲ)求平面AFC1与与平面ABCD所成二面角的大小。
18、(本小题满分12分)
已知二次函数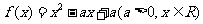 ,不等式
,不等式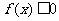 的解集有且只有一个元素,设数列
的解集有且只有一个元素,设数列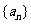 的前
的前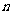 项和
项和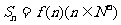
(Ⅰ)求数列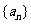 的通项公式; (Ⅱ)设
的通项公式; (Ⅱ)设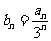 ,求数列
,求数列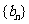 的前
的前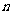 项和
项和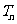 .
.
17、(本小题满分10分)
设函数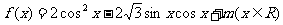 。
。
(Ⅰ)求函数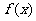 的最小正周期及函数的单调递增区间 ;
的最小正周期及函数的单调递增区间 ;
(Ⅱ)若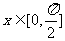 ,是否存在实数m,使函数
,是否存在实数m,使函数 ?若存在,请求出m的取值;若不存在,请说明理由。
?若存在,请求出m的取值;若不存在,请说明理由。
16、已知圆M:(x+cosq)2+(y-sinq)2=1,直线l:y=kx,下面四个命题:
①对任意实数k与q,直线l和圆M相切;
②对任意实数k与q,直线l和圆M有公共点;
③对任意实数q,必存在实数k,使得直线l与和圆M相切;
④对任意实数k,必存在实数q,使得直线l与和圆M相切。
其中真命题的代号是______________(写出所有真命题的代号)。
15、已知正四面体S-ABC中,点E为SA的中点,点F为△ABC的中心,则异面直线EF、AB所成的角为 。
14、在抽查产品的尺寸过程中,将其尺寸分成若干组,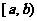 是其中一组,抽查出的个体在该组上的频率为0.2,该组上的直方图的高为2。则
是其中一组,抽查出的个体在该组上的频率为0.2,该组上的直方图的高为2。则 =
。
=
。
13、若正数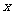 、
、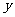 满足
满足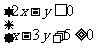 则
则 的最大值为 。
的最大值为 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com