
1.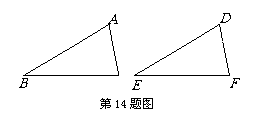 (2010山东济南)如图所示,△DEF是△ABC沿水平方向向右平移后的对应图形,若∠B=31°,∠C=79°,则∠D的度数是
度.
(2010山东济南)如图所示,△DEF是△ABC沿水平方向向右平移后的对应图形,若∠B=31°,∠C=79°,则∠D的度数是
度.
答案: 70
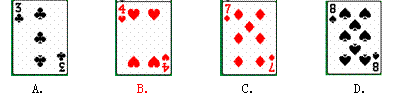
1.(2010宁德)下列四张扑克牌图案,属于中心对称的是( ).B
1、(2010年泉州南安市)请写出一个既是轴对称,又是中心对称的几何图形名称:
答案:如:矩形(答案不惟一)
(2010年天津市)(2)下列图形中,既可以看作是轴对称图形,又可以看作是中心对称图形的为(B)

(A) (B) (C) (D)
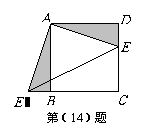 (2010年天津市)(14)如图,已知正方形
(2010年天津市)(14)如图,已知正方形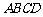 的边长为3,
的边长为3,
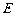 为
为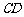 边上一点,
边上一点, 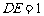 .以点
.以点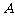 为中心,把△
为中心,把△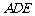 顺时
顺时
针旋转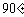 ,得△
,得△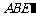 ,连接
,连接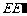 ,则
,则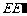 的长等于
的长等于 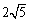 .
.
(2010年天津市)(18)有一张矩形纸片ABCD,按下面步骤进行折叠:
第一步:如图①,将矩形纸片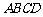 折叠,使点B、D重合,点C落在点
折叠,使点B、D重合,点C落在点 处,得折痕EF;
处,得折痕EF;
第二步:如图②,将五边形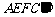 折叠,使AE、
折叠,使AE、 重合,得折痕DG,再打开;
重合,得折痕DG,再打开;
第三步:如图③,进一步折叠,使AE、 均落在DG上,点A、
均落在DG上,点A、 落在点
落在点 处,点E、F落在点
处,点E、F落在点 处,得折痕MN、QP.
处,得折痕MN、QP.
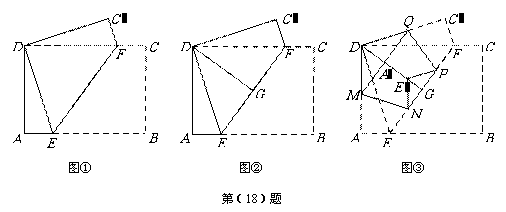 这样,就可以折出一个五边形
这样,就可以折出一个五边形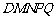 .
.
(Ⅰ)请写出图①中一组相等的线段 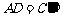 (答案不惟一,也可以是
(答案不惟一,也可以是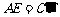 等)(写出一组即可);
等)(写出一组即可);
(Ⅱ)若这样折出的五边形DMNPQ(如图③)恰好是一个正五边形,当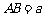 ,
,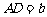 ,
,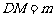 时,有下列结论:
时,有下列结论:
①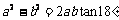 ; ②
; ②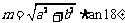 ;
;
③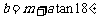 ; ④
; ④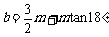 .
.
其中,正确结论的序号是 ①②③ (把你认为正确结论的序号都填上).
(2010年天津市)(25)(本小题10分)
在平面直角坐标系中,矩形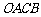 的顶点O在坐标原点,顶点A、B分别在
的顶点O在坐标原点,顶点A、B分别在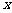 轴、
轴、
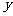 轴的正半轴上,
轴的正半轴上,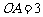 ,
,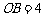 ,D为边OB的中点.
,D为边OB的中点.
 (Ⅰ)若
(Ⅰ)若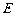 为边
为边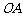 上的一个动点,当△
上的一个动点,当△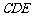 的周长最小时,求点
的周长最小时,求点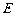 的坐标;
的坐标;
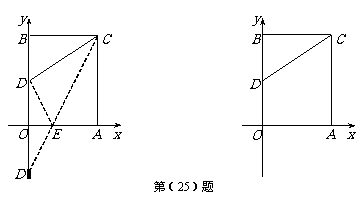
(Ⅱ)若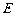 、
、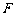 为边
为边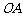 上的两个动点,且
上的两个动点,且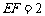 ,当四边形
,当四边形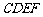 的周长最小时,求点
的周长最小时,求点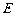 、
、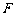 的坐标.
的坐标.
解:(Ⅰ)如图,作点D关于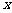 轴的对称点
轴的对称点 ,连接
,连接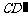 与
与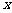 轴交于点E,连接
轴交于点E,连接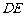 .
.
若在边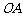 上任取点
上任取点 (与点E不重合),连接
(与点E不重合),连接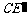 、
、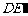 、
、 .
.
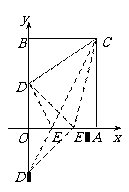 由
由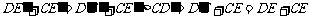 ,
,
可知△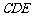 的周长最小.
的周长最小.
∵ 在矩形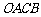 中,
中,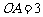 ,
,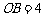 ,
,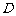 为
为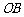 的中点,
的中点,
∴ 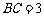 ,
,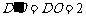 ,
, .
.
∵ OE∥BC,
∴ Rt△ ∽Rt△
∽Rt△ ,有
,有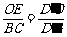 .
.
∴ 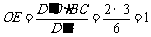 .
.
∴ 点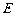 的坐标为(1,0). ................................6分
的坐标为(1,0). ................................6分
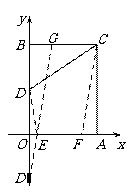 (Ⅱ)如图,作点
(Ⅱ)如图,作点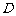 关于
关于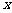 轴的对称点
轴的对称点 ,在
,在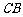 边上截取
边上截取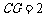 ,连接
,连接 与
与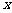 轴交于点
轴交于点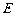 ,在
,在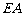 上截取
上截取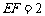 .
.
∵ GC∥EF,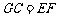 ,
,
∴ 四边形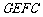 为平行四边形,有
为平行四边形,有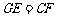 .
.
又 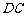 、
、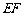 的长为定值,
的长为定值,
∴ 此时得到的点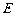 、
、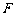 使四边形
使四边形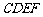 的周长最小.
的周长最小.
∵ OE∥BC,
∴ Rt△ ∽Rt△
∽Rt△ , 有
, 有 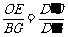 .
.
∴ 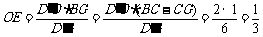 .
.
∴ 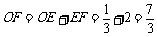 .
.
∴ 点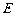 的坐标为(
的坐标为(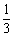 ,0),点
,0),点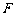 的坐标为(
的坐标为(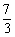 ,0). ...............10分
,0). ...............10分
(2010年天津市)(26)(本小题10分)
在平面直角坐标系中,已知抛物线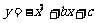 与
与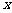 轴交于点
轴交于点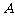 、
、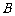 (点
(点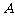 在点
在点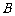 的左侧),与
的左侧),与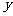 轴的正半轴交于点
轴的正半轴交于点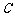 ,顶点为
,顶点为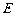 .
.
(Ⅰ)若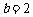 ,
,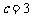 ,求此时抛物线顶点
,求此时抛物线顶点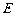 的坐标;
的坐标;
(Ⅱ)将(Ⅰ)中的抛物线向下平移,若平移后,在四边形ABEC中满足
S△BCE = S△ABC,求此时直线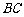 的解析式;
的解析式;
(Ⅲ)将(Ⅰ)中的抛物线作适当的平移,若平移后,在四边形ABEC中满足
S△BCE = 2S△AOC,且顶点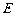 恰好落在直线
恰好落在直线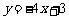 上,求此时抛物线的解析式.
上,求此时抛物线的解析式.
解:解:(Ⅰ)当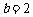 ,
,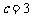 时,抛物线的解析式为
时,抛物线的解析式为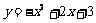 ,即
,即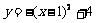 .
.
∴ 抛物线顶点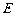 的坐标为(1,4).
.................2分
的坐标为(1,4).
.................2分
(Ⅱ)将(Ⅰ)中的抛物线向下平移,则顶点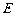 在对称轴
在对称轴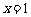 上,有
上,有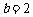 ,
,
∴ 抛物线的解析式为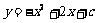 (
(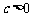 ).
).
∴ 此时,抛物线与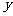 轴的交点为
轴的交点为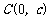 ,顶点为
,顶点为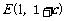 .
.
∵ 方程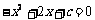 的两个根为
的两个根为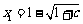 ,
,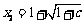 ,
,
∴ 此时,抛物线与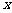 轴的交点为
轴的交点为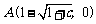 ,
,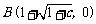 .
.
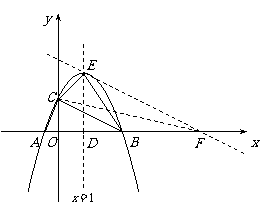 如图,过点
如图,过点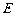 作EF∥CB与
作EF∥CB与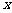 轴交于点
轴交于点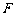 ,连接
,连接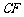 ,则S△BCE = S△BCF.
,则S△BCE = S△BCF.
∵ S△BCE = S△ABC,
∴ S△BCF = S△ABC.
∴ 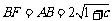 .
.
设对称轴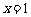 与
与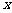 轴交于点
轴交于点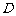 ,
,
则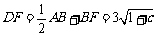 .
.
由EF∥CB,得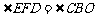 .
.
∴ Rt△EDF∽Rt△COB.有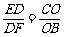 .
.
∴ 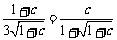 .结合题意,解得
.结合题意,解得 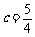 .
.
∴ 点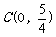 ,
,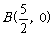 .
.
设直线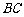 的解析式为
的解析式为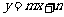 ,则
,则
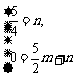 解得
解得
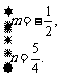
∴ 直线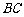 的解析式为
的解析式为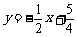 .
.........................6分
.
.........................6分
(Ⅲ)根据题意,设抛物线的顶点为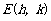 ,(
,(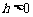 ,
,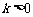 )
)
则抛物线的解析式为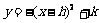 ,
,
此时,抛物线与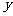 轴的交点为
轴的交点为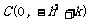 ,
,
与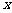 轴的交点为
轴的交点为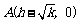 ,
,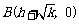 .(
.(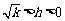 )
)
过点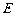 作EF∥CB与
作EF∥CB与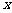 轴交于点
轴交于点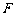 ,连接
,连接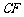 ,
,
则S△BCE = S△BCF.
由S△BCE = 2S△AOC,
∴ S△BCF = 2S△AOC. 得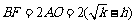 .
.
设该抛物线的对称轴与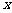 轴交于点
轴交于点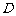 .
.
则 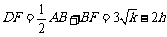 .
.
于是,由Rt△EDF∽Rt△COB,有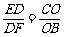 .
.
∴ 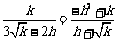 ,即
,即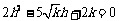 .
.
结合题意,解得 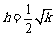 .
①
.
①
∵ 点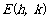 在直线
在直线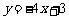 上,有
上,有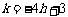 . ②
. ②
∴ 由①②,结合题意,解得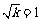 .
.
有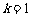 ,
,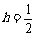 .
.
∴ 抛物线的解析式为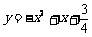 . .........................10分
. .........................10分
(2010山西20.(本题6分)山西民间建筑的门窗图案中,隐含着丰富的数学艺术之美.图1是其中一个代表,该窗格图案是以图2为基本图案经过图形变换得到的.图3是图2放大后的部分,虚线给出了作图提示,请用圆规和直尺画图.
(1)根据图2将图3补充完整;
(2)在图4的正方形中,用圆弧和线段设计一个美观的轴对称或中心对称图形.
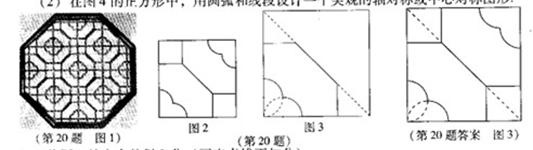
(1) 将图3补充完整得3分(画出虚线不扣分)
(2) 图略,答案不唯一,只要符合题目要求均得3分
2.(10湖南怀化)下列图形中,是中心对称图形但不是轴对称图形的是( )B

19.答案如图 每个图形3分
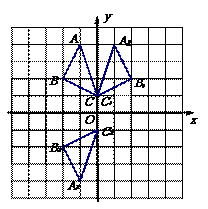
 毕节13.正方形ABCD在坐标系中的位置如图所示,将正方形ABCD
毕节13.正方形ABCD在坐标系中的位置如图所示,将正方形ABCD
绕D点顺时针方向旋转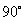 后,B点的坐标为( D )
后,B点的坐标为( D )
A.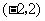 B.
B.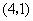 C.
C.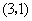 D.
D.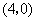
19. (2010年郴州市)
(2010年郴州市)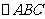 在平面直角坐标系中的位置如图所示,将
在平面直角坐标系中的位置如图所示,将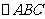 沿y轴翻折得到
沿y轴翻折得到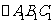 ,再将
,再将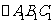 绕点O旋转
绕点O旋转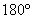 得到
得到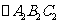 . 请依次画出
. 请依次画出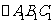 和
和 .
.
答案:
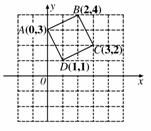
13.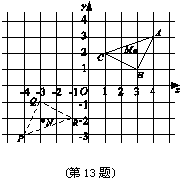 (2010年济宁市)如图,
(2010年济宁市)如图,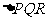 是
是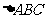 经过某种变换后得到的图形.如果
经过某种变换后得到的图形.如果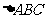 中任意一点
中任意一点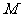 的坐标为(
的坐标为(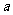 ,
,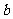 ),那么它的对应点
),那么它的对应点 的坐标为
.
的坐标为
.
答案:( ,
, );
);
2.(2010年怀化市)下列图形中,是中心对称图形但不是轴对称图形的是( )
答案:B
3.(2010宁波市)下列各图是选择自历届世博会会徽中的图案,其中是中心对称图形的是 C
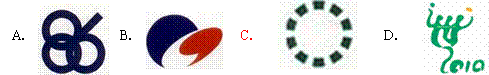
24.(2010年连云港)(本题满分10分)如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转,试解决下列问题:
 (1)画出四边形ABCD旋转后的图形;
(1)画出四边形ABCD旋转后的图形;
(2)求点C旋转过程事所经过的路径长;
(3)设点B旋转后的对应点为B’,求tan∠DAB’的值.
|

答案
(2)易知点C的旋转路径是以为O圆心,OC为半径的半圆
因为OC=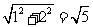 ,所以半圆的周长为
,所以半圆的周长为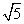 π
.............................................6分
π
.............................................6分
(3)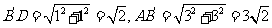 ,
,
所以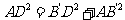
所以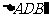 是直角三角形,且
是直角三角形,且 ..............................................................8分
..............................................................8分
所以tan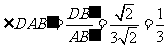 .............................................................................10分
.............................................................................10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com