10.如图为某三角函数图象的一段

(1)用正弦函数写出其中一个解析式；

(2)求与这个函数关于直线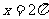对

称的函数解析式，并作出它一个周期内简图。

思路分析：由，由最值定A，由特殊值定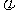，用五点法作简图。

解：(1)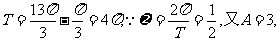

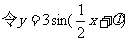由图它过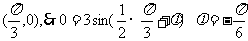(为其中一个值)

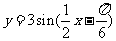
(2)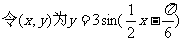上任意一点，该点关于直线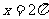对称点为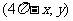

关于直线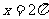对称的函数解析式是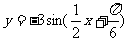

列表：

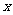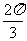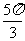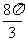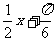	0
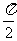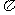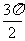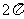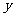	0	-3	0	3	0

作图：

[探索题](2005全国Ⅰ)设函数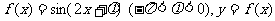图像的一条对称轴是直线。

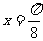(Ⅰ)求；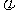

(Ⅱ)求函数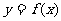的单调增区间；

(Ⅲ)证明直线与函数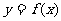的图像不相切。

解：(Ⅰ)的图像的对称轴，

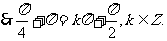
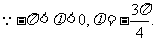
(Ⅱ)由(Ⅰ)知

由题意得

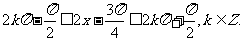
所以函数

(Ⅲ)证明：∵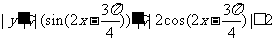

所以曲线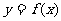的切线斜率的取值范围为[-2,2]，

而直线的斜率为，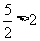

所以直线于函数的图像不相切

9. (2003季上海)已知函数f(x)=Asin(ωx+φ),

x∈R(其中A>0,ω>0)在一个周期内的图象如图

所示。求直线y=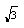与函数f(x)图象的所有交点

的坐标

[解]根据图象得A=2,T=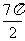-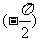=4π,ω=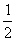

,又由图象可得相位移为,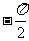

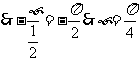.即,

根据条件:,

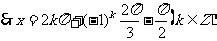
[思维点拨]按图可求得f(x)=Asin(ωx+φ)，再求交点即可。

8.(2006福建) 已知函数

　　　 (I)求函数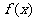的最小正周期和单调增区间；

　　　 (II)函数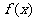的图象可以由函数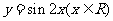的图象经过怎样的变换得到？

　　　 解：(I)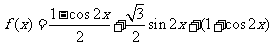

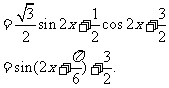
　　　 的最小正周期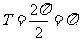

　　　 由题意得

　　　 即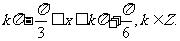　

　　　 的单调增区间为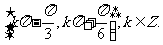

　　　 (II)方法一：

　　　 先把图象上所有点向左平移个单位长度，得到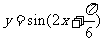的图象，再把所得图象上所有的点向上平移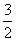个单位长度，就得到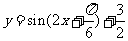的图象。

　　　 方法二：

　　　 把图象上所有的点按向量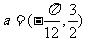平移，就得到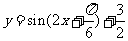的图象。

7. (2006山东)已知函数，且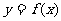的最大值为2，其图象相邻两对称轴间的距离为2，并过点(1,2).

(I)求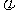

(II)计算.

解：(I)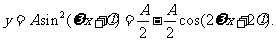

的最大值为2，.

又其图象相邻两对称轴间的距离为2，，

.

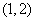过点，

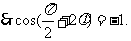
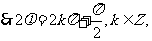
又

.

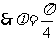(II)解法一：，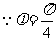

.

又的周期为4，，

解法二：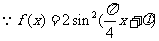

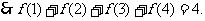
又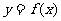的周期为4，，

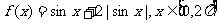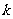6.(2005上海)函数的图象与直线有且仅有两个不同的交点，则的取值范围是__________。

✿练习简答：1-4.DACA；5. (1，); 6. .

[解答题]

5.(2006湖南)若是偶函数, 则有序实数对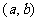可以是__________.(注: 写出你认为正确的一组数字即可)