
3.会用分析法证明较复杂的代数不等式..

冲刺强化训练(7)
2.掌握应用问题处理的基本步骤;
1.学会数形相互转化;
例1..已知函数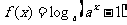 (a>0且a≠1)
(a>0且a≠1)
(1)证明: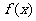 的图象在y轴一侧;
的图象在y轴一侧;
(2) 设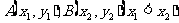 是
是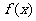 图象上两点,证明:AB的斜率大于0;
图象上两点,证明:AB的斜率大于0;
(3)函数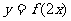 与图象
与图象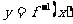 的交点坐标
的交点坐标




例2.如图,两铁路线垂直相交于站A,若已知AB=100千米,甲火车从A站出发,沿AC方向以50千米/小时的速度行驶,同时乙火车以v千米/小时的速度从B站沿BA方向行驶致A站即停止前行(甲车仍继续行驶)
(1)求甲,乙两车的最近距离(两车的车长忽略不计)
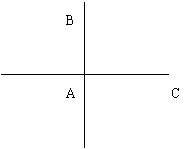 (2)若甲,乙两车开始行驶到甲,乙两车相距最近所用时间为
(2)若甲,乙两车开始行驶到甲,乙两车相距最近所用时间为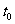 小时,问v为何值时
小时,问v为何值时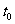 最大?
最大?





例3.已知函数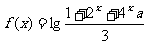

(1)若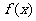 在
在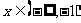 时恒有意义,求实数a的取值范围;
时恒有意义,求实数a的取值范围;
(2)当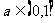 ,且
,且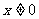 时,求证:
时,求证: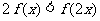






5.已知函数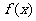 满足:
满足: ,
,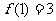

则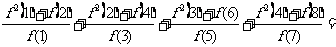

4.关于x的方程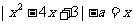 有三个不相等的实数根,则实数a的值是
有三个不相等的实数根,则实数a的值是

3.在区间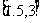 上,函数
上,函数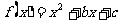 与函数
与函数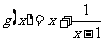 同时取到相同的最小值,则函数
同时取到相同的最小值,则函数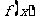 在区间
在区间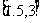 上的最大值为 ( )
上的最大值为 ( )
A 8 B 6 C 5 D 4
2.设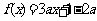 在
在 上存在
上存在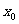 ,使
,使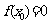 ,则a的范围是 ( )
,则a的范围是 ( ) 
A 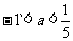 B
B 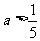 C
C 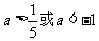 D a<-1
D a<-1
1.函数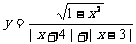 的图象关于 ( )
的图象关于 ( )
A
x轴对称 B 直线y=x对称
C 原点对称 D y轴对称
2.掌握应用问题处理的一般步骤,培养应用意识,体会各种数学思想方法的运用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com