
1、甲乙两车在平直道路上同向运动,其v--t图象如
图所示,图中ΔOPQ和ΔOQT的面积分别为S1和S2
(S2>S1),初始时甲车在乙车前方S0处( )
A:若S0=S1+S2,两车不会相遇。
B:若S0<S1,两车相遇2次。
C:若S0=S1,两车相遇1次。
D:若S0=S2 ,两车相遇1次。
,两车相遇1次。
22、已知数列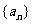 满足
满足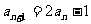 且
且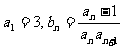 ,数列
,数列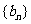 的前n项和为
的前n项和为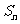 ,
,
(1)求证:数列 是等比数列;
是等比数列;
(2)求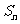 ;
;
(3)设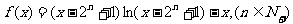 ,求证:
,求证: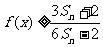 。
。
解(1)由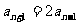 得
得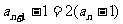 且
且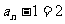
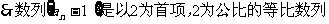
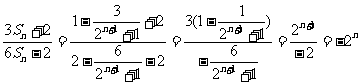
(2)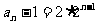
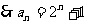
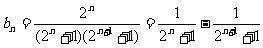

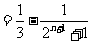
(3) 
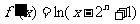
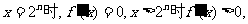
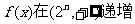
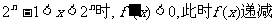

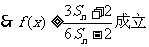
21、设函数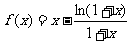 ,
,
(1)令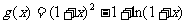 ,判断并证明
,判断并证明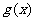 在
在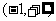 上的单调性,并求
上的单调性,并求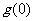 ;
;
(2)求函数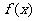 的最小值;
的最小值;
(3)是否存在实数m,n,满足-1<m<n,使得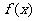 在区间[m,n]上的值域也为[m,n]。
在区间[m,n]上的值域也为[m,n]。

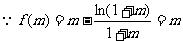

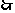
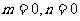 与m<n矛盾
与m<n矛盾
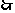 不存在这样的实数m,n
不存在这样的实数m,n
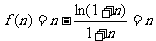
20、在平面内有两个向量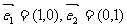 ,今有动
,今有动 点P从
点P从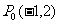 开始沿着与向量
开始沿着与向量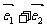 相同方向做匀速直线运动,速度为︱
相同方向做匀速直线运动,速度为︱
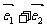 ︱;另一动点Q从点
︱;另一动点Q从点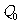 (-2,-1)出发,沿着与向量
(-2,-1)出发,沿着与向量
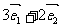 相同的方向做匀速直线运动,速度为︱
相同的方向做匀速直线运动,速度为︱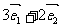 ︱,设点P、Q在时刻t=0秒时分别在
︱,设点P、Q在时刻t=0秒时分别在
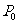 、
、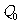 处,求PQ⊥
处,求PQ⊥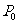
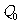 时,用了多长时间
时,用了多长时间
解: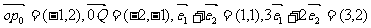
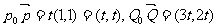
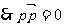
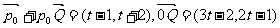
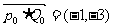 .
.
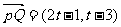
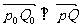


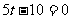
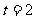 (秒)
(秒)
用了2秒
19、已知向量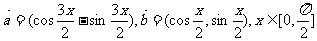 ,函数
,函数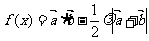
(1)若 ,求方程
,求方程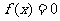 的根;
的根;
(2)若函数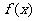 的最小值为
的最小值为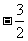 ,求实数
,求实数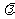 的值。
的值。
解:(1)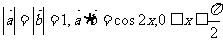
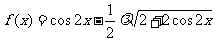
=cos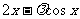
当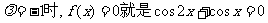
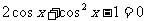
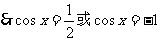
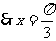
(2),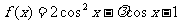
=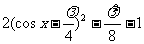
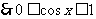
1,当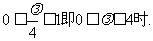 3,当
3,当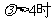
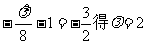 当
当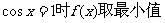
2,当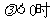
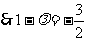 得
得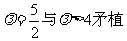
当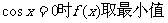 得上
得上 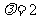
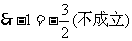
18、已知锐角△ABC中,角A.B.C所对边分别是a.b.c,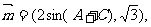
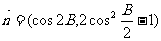 ,且
,且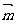 ∥
∥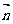
(3) 求角B的大小;
(4) 如果b=1,求△ABC面积的最大值。

17、数列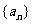 的前n项和记为
的前n项和记为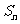 ,
,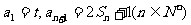
(1)t为何值时,数列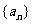 是等比数列?
是等比数列?
(2)在(1)的条件下,若等差数列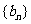 的前n项和
的前n项和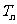 有最大值,且
有最大值,且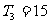 ,又
,又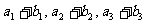 成等比数列,求
成等比数列,求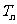 。
。
解:(1)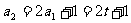
n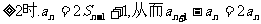
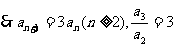
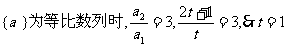
(2)设等差数列{bn}的合差为d(d<0),由T3=15,得b2=5,而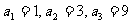
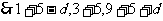 成等比数列 (b-d)(d+14)=82
成等比数列 (b-d)(d+14)=82
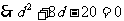
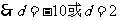
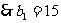
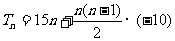
=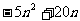
15、
169
16、 ①、③ 
13、 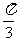 14、 33
14、 33
22、已知数列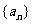 满足
满足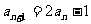 且
且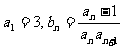 ,数列
,数列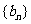 的前n项和为
的前n项和为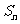 ,
,
(1)求证:数列 是等比数列;
是等比数列;
(2)求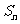 ;
;
(3)设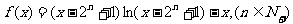 ,求证:
,求证: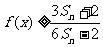 。
。
 靖安中学高三年级10月月考数学答卷(理)
靖安中学高三年级10月月考数学答卷(理)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com