5.碰撞中的动量守恒

(1)每次入射小球都应该从斜槽轨道的同一位置开始自由下滑。

(2)被碰小球的位置必须与入射小球等高，其中心与斜槽末端的水平距离恰好是小球半径的2倍。

(3)由于v₁、v₁^/、v₂^/ 均为水平方向，且两球的竖直下落高度相等，所以它们飞行时间相等，若以该时间为时间单位，那么小球的水平射程的数值就等于它们的水平速度。在右图中分别用OP、OM和O ^/N表示。因此只需验证：m₁žOP=m₁žOM+m₂ž(O ^/N-2r)即可。

(4)必须以质量较大的小球作为入射小球(保证碰撞后两小球都向前运动)。

(5)小球落地点的平均位置要用圆规来确定：用尽可能小的圆把所有落点都圈在里面，圆心就是落点的平均位置。

(6)所用的仪器有：天平、刻度尺、游标卡尺(测小球直径)、碰撞实验器、复写纸、白纸、重锤、两个直径相同质量不同的小球、圆规。

(7)若被碰小球放在斜槽末端，而不用支柱，那么两小球将不再同时落地，但两个小球都将从斜槽末端开始做平抛运动，于是验证式就变为：m₁žOP=m₁žOM+m₂žON，两个小球的直径也不需测量了(但必须相等)。

例6 在“碰撞中的动量守恒”实验中，仪器按要求安装好后开始实验，第一次不放被碰小球，第二次把被碰小球直接静止放在斜槽末端的水平部分，在百纸上记录下重锤位置和各小球落点的平均位置依次为O、A、B、C，设入射小球和被碰小球的质量依次为m₁、m₂，则下列说法中正确的有

A.第一、二次入射小球的落点依次是A、B

B.第一、二次入射小球的落点依次是B、A

C.第二次入射小球和被碰小球将同时落地

D. m₁　AB= m₂　OC

解：最远的C点一定是被碰小球的落点，碰后入射小球的速度将减小，因此选B；由于被碰小球是放在斜槽末端的，因此被碰小球飞出后入射小球才可能从斜槽末端飞出，两小球不可能同时落地；由动量守恒得m₁　OB= m₁　OA+m₂　OC，选D。答案是BD。

4.验证牛顿第二运动定律

(1)了解该实验的系统误差的来源。

①用砂和砂桶的总重量代替小车受到的拉力。由牛顿第二定律可知，由于砂桶也在做匀加速运动，因此砂和砂桶的总重量肯定大于小车受到的实际拉力。可以推导出结论：只有在小车的总质量M远大于砂和砂桶的总质量m时，才能使该系统误差足够小。

②没有考虑摩擦阻力的作用。应该用平衡摩擦力的方法来消除这个系统误差。

(2)为研究a、F、m三者的关系，要利用“控制变量法”，分别研究a与F、 a与m的关系。

(3)用图象法验证a∝F、 a∝m^-1(后者必须用a-m^-1图象，不能用a-m图象)

例5 一打点计时器固定在斜面上某处，一小车拖着穿过打点计时器的纸带从斜面上滑下，如右图所示。下图是打出的纸带的一段。

⑴已知打点计时器使用的交流电频率为50Hz，利用下图给出的数据可求出小车下滑的加速度a=_____。

⑵为了求出小车在下滑过程中所受的阻力，还需要测量的物理量有_______。用测得的量及加速度a表示阻力的计算式为f=_________。

解： (1)3.89m/s²

(2)小车质量m；斜面上任意两点间距离l及这两点的高度差h。mgh/l-ma

3.测定匀变速直线运动的加速度

(1)纸带处理。从打点计时器重复打下的多条纸带中选点迹　 清楚的一条，舍掉开始比较密集的点迹，从便于测量的地方取一个开始点O，然后每5个点取一个计数点A、B、C、…(或者说每隔4个点取一个记数点)，这样做的好处是相邻记数点间的时间间隔是0.1s，便于计算。测出相邻计数点间的距离s₁、s₂、s₃ …

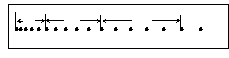
(2)利用s₁、s₂、s₃ …可以计算相邻相等时间内的位移差s₂-s₁、s₃- s₂、s₄- s₃…，如果它们在允许的误差范围内相等，则可以判定被测物体的运动是匀变速直线运动。

(3)利用纸带可以求被测物体在任一计数点对应时刻的瞬时速度v：如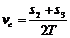　

(4)利用纸带求被测物体的加速度a。具体来说又有3种方法：

　 ①“逐差法”：从纸带上得到6个相邻相等时间内的位移，则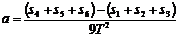

　 ②利用任意两段相邻记数点间的位移求a：如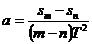

　 ③利用v-t图象求a：求出A、B、C、D、E、F各点的即时速度，画出如右的v-t图线，图线的斜率就是加速度a。

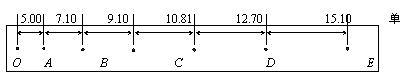例4 某同学在做“测定匀变速直线运动的加速度”实验时，从打下的若干纸带中选出了如图所示的一条(每两点间还有4个点没有画出来)，图中上部的数字为相邻两个计数点间的距离。打点计时器的电源频率为50Hz。

　　 由这些已知数据计算：①该匀变速直线运动的加速度a=___________m/s²。②与纸带上D点相对应的瞬时速度v=__________ m/s。(答案均要求保留3位有效数字)

2.互成角度的两个共点力的合成

(1)原理是两只弹簧秤成角度拉橡皮条AB和一只弹簧秤拉　 橡皮条AB的效果相同，这个效果就是指橡皮条的形变量(大小和方向)相同。

(2)在画力的图示时，必须有箭头、标度、刻度。

(3)实验往往有一定的偶然误差，只要用平行四边形定则求得的合力F和一只弹簧秤的拉力F ^/ 的图示大小和方向在误差允许的范围内相同就可以了。

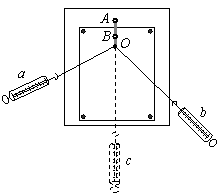
例3 橡皮筋的一端固定在A点，另一端栓上两根细绳，每根细绳分别连着一个量程为5N、最小刻度为0.1N的弹簧测力计，沿着两个不同的方向拉弹簧测力计。当橡皮筋的活动端拉到O点时，两根细绳相互垂直，如图所示。这时弹簧测力计的读数可从图中读出。⑴由图可读得两个相互垂直的拉力的大小分别为_____N和_____N。(只须读到0.1N)⑵在右图的方格纸中按作图法的要求画出这两个力及它们的合力。

解：(1)2.5N和4.0N

(2)注意平行四边形中的实线、虚线的区别和箭头、标度、单位。

1.长度的测量(游标卡尺和螺旋测微器)

(1)游标卡尺

①10分度的游标卡尺。游标上相邻两个刻度间的距离为0.9mm，比主尺上相邻两个刻度间距离小0.1mm。读数时先从主尺上读出厘米数和毫米数，然后用游标读出0.1毫米位的数值：游标的第几条刻线跟主尺上某一条刻线对齐，0.1毫米位就读几(不能读某)。其读数准确到0.1mm。

②20分度的游标卡尺。游标上相邻两个刻度间的距离为0.95mm，比主尺上相邻两个刻度间距离小0.05mm。读数时先从主尺上读出厘米数和毫米数，然后用游标 读出毫米以下的数值：游标的第几条刻线跟主尺上某一条刻线对齐，毫米以下的读数就是几乘0.05毫米。其读数准确到0.05mm。

③50分度的游标卡尺。游标上相邻两个刻度间的距离为0.98mm，比主尺上相邻两个刻度间距离小0.02mm。这种卡尺的刻度是特殊的，游标上的刻度值，就是毫米以下的读数。这种卡尺的读数可以准确到0.02mm。

注意：游标卡尺都是根据刻线对齐来读数的， 所以都不再往下一位估读。

要知道主要构造的名称：主尺、游标尺、外测量爪、内测量爪、深度尺、紧固螺钉。

(2)螺旋测微器

固定刻度上的最小刻度为0.5mm(在中线的上侧)；可动刻度每旋转一圈前进(或后退)0.5mm。在可动刻度的一周上平均刻有50条刻线，所以相邻两条刻线间代表0.01mm。读数时，从固定刻度上读取整、半毫米数，然后从可动刻度上读取剩余部分(因为是10分度，所以在最小刻度后必须再估读一位)，再把两部分读数相加，得测量值。

要知道主要构造的名称：以下的①-⑦依次是：测砧、测微螺杆、固定刻度、可动刻度、旋钮、微调旋钮和尺架。

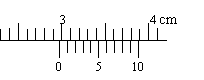
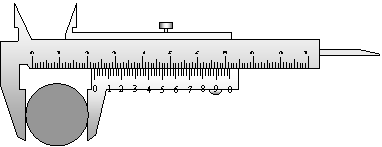
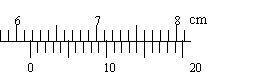例1 读出下列游标卡尺测量的读数。

⑴　　　　　　　　　　　　　　 ⑵

⑶

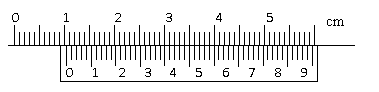
解：(1)2.98cm；(2)6.170cm；(3)1.050cm

例2 读出下列螺旋测微器测量的读数。

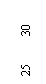
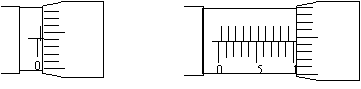⑴　　　　　　　　　　　　 ⑵

解：(1)0.642mm ；(2)10.294mm

2.有效数字

带有一位不可靠数字的近似数字，叫做有效数字。

(1)有效数字是指近似数字而言。

(2)只能带有一位不可靠数字，不是位数越多越好。

注：凡是用测量仪器直接测量的结果，读数一般要求在读出仪器最小刻度所在位的数值(可靠数字)后，再向下估读一位(不可靠数字)，这里不受有效数字位数的限制。间接测量的有效数字运算不作要求，运算结果一般可用2_~3位有效数字表示。

1.误差

测量值与真实值的差异叫做误差。误差可分为系统误差和偶然误差两种。

(1)系统误差的特点是在多次重复同一实验时，误差总是同样地偏大或偏小。

(2)偶然误差总是有时偏大，有时偏小，并且偏大和偏小的机会相同。减小偶然误差的方法，可以多进行几次测量，求出几次测量的数值的平均值。这个平均值比某一次测得的数值更接近于真实值。

11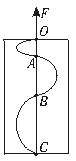．如图所示，一块质量为2 kg、涂有碳黑的玻璃板，在拉力F的作用下竖直向上做匀变速直线运动．一个频率为5 Hz的振动方向为水平且固定的振针，在玻璃板上画出了如图所示的图线，量得OA=1 cm，OB=4 cm，OC=9 cm．求拉力F的大小． (不计一切摩擦阻力，取g=10 m/s²)

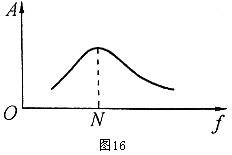
10． 如图16是某物体的共振曲线，若是悬挂在天花板上的单摆的共振曲线，则其摆长为L=__________(设g为已知)

9． 如图所示，在竖直平面内有一段光滑圆轨道MN，它所对的圆心角小于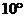，P点是MN的中点，也是圆弧的最低点。在N　 P之间的点Q和P之间搭一光滑斜面，将一小滑块(可视为质点)分别从Q点和M点由静止开始释放，设圆半径为R，则两次运动到P点所需的时间分别为__________、__________。