
(一)选择题
1.某班元旦联欢会原定的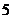 个学生节目已排成节目单,开演前又增加了两个教师节目。如果将这两个教师节目插入原节目单中,那么不同插法的种数为
(A)
个学生节目已排成节目单,开演前又增加了两个教师节目。如果将这两个教师节目插入原节目单中,那么不同插法的种数为
(A)
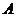 .
.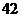
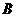 .
.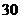
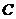 .
.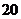
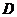 .
.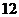
2.从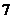 人中选派
人中选派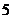 人到
人到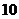 个不同的交通岗的
个不同的交通岗的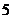 个中参加交通协管工作,则不同的选派方法
个中参加交通协管工作,则不同的选派方法
有 (D)
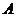 .
.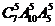
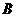 .
.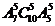
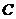 .
.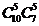
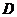 .
.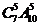
3.某班分成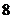 个小组,每小组
个小组,每小组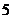 人,现要从中选出
人,现要从中选出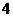 人进行
人进行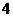 个不同的化学实验,且每组至多选一人,则不同的安排方法种数是
(C)
个不同的化学实验,且每组至多选一人,则不同的安排方法种数是
(C)
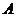 .
.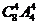
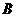 .
.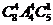
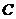 .
.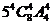
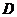 .
.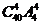
5.按指定的一种顺序排列的问题,实质是组合问题。
4.需要注意的是,均匀分组(不计组的顺序)问题不是简单的组合问题,如:将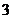 个人分成
个人分成
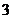 组,每组一个人,显然只有
组,每组一个人,显然只有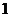 种分法,而不是
种分法,而不是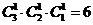 种
。一般地,将
种
。一般地,将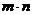 个
个
不同元素均匀分成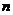 组,有
组,有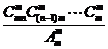 种分法;
种分法;
3.对于含“至多”、“至少”的问题,宜用排除法或分类解决;
2.对于有限制条件的问题,要优先安排特殊元素、特殊位置;
1.按元素的性质进行分类、按事件发生的连续过程分步,是处理组合应用题的基本思想方
法;
(二)新课讲解:
例1 6本不同的书,按下列要求各有多少种不同的选法:
(1)分给甲、乙、丙三人,每人2本;
(2)分为三份,每份2本;
(3)分为三份,一份1本,一份2本,一份3本;
(4)分给甲、乙、丙三人,一人1本,一人2本,一人3本;
(5)分给甲、乙、丙三人,每人至少1本。
解:(1)根据分步计数原理得到: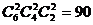 种;
种;
(2)分给甲、乙、丙三人,每人两本有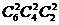 种方法,这个过程可以分两步完成:第一步分为三份,每份两本,设有x种方法;第二步再将这三份分给甲、乙、丙三名同学有
种方法,这个过程可以分两步完成:第一步分为三份,每份两本,设有x种方法;第二步再将这三份分给甲、乙、丙三名同学有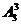 种方法.根据分步计数原理可得:
种方法.根据分步计数原理可得: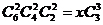 ,所以
,所以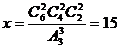 .
.
因此,分为三份,每份两本一共有15种方法。
说明:本题是分组中的“均匀分组”问题.
一般地:将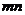 个元素均匀分成
个元素均匀分成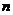 组(每组
组(每组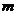 个元素),共有
个元素),共有
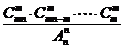 种方法。
种方法。
(3)这是“不均匀分组”问题,一共有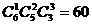 种方法.
种方法.
(4)在(3)的基础上再进行全排列,所以一共有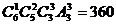 种方法.
种方法.
(5)可以分为三类情况:①“2、2、2型”即(1)中的分配情况,有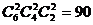 种方法;②“1、2、3型”即(4)中的分配情况,有
种方法;②“1、2、3型”即(4)中的分配情况,有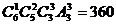 种方法;③“1、1、4型”,有
种方法;③“1、1、4型”,有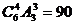 种方法,
种方法,
所以,一共有90+360+90=540种方法.
例2 身高互不相同的7名运动员站成一排,
(1)其中甲、乙、丙三人自左向右从高到矮排列的排法有多少种?
(2)其中甲、乙、丙三人自左向右从高到矮排列且互不相邻的排法有多少种?
解:(1)(法一):设想有7个位置,先将其他4人排好,有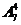 种排法;再将甲、乙、丙三人自左向右从高到矮排在剩下的3个位置上,只有1种排法,根据分步计数原理,一共有
种排法;再将甲、乙、丙三人自左向右从高到矮排在剩下的3个位置上,只有1种排法,根据分步计数原理,一共有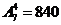 种方法。
种方法。
(法二):设想有7个位置,先将甲、乙、丙三人自左向右从高到矮排在其中的3个位置上,有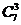 种排法;将其他4人排在剩下的4个位置上,有
种排法;将其他4人排在剩下的4个位置上,有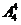 种排法;根据分步计数原理,一共有
种排法;根据分步计数原理,一共有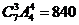 种方法.
种方法.
(2)(插空法)先将其余4个同学进行全排列一共有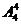 种方法,再将甲、乙、丙三名同学插入5个空位置中(但无需要进行排列)有
种方法,再将甲、乙、丙三名同学插入5个空位置中(但无需要进行排列)有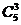 种方法.根据分步计数原理,一共有
种方法.根据分步计数原理,一共有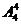
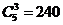 种方法.
种方法.
例3 (1) 四个不同的小球放入四个不同的盒中,一共有多少种不同的放法?
(2) 四个不同的小球放入四个不同的盒中且恰有一个空盒的放法有多少种?
解:(1)根据分步计数原理:一共有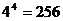 种方法;
种方法;
(2)(捆绑法)第一步:从四个不同的小球中任取两个“捆绑”在一起看成一个元素有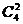 种方法;第二步:从四个不同的盒中任取三个将球放入有
种方法;第二步:从四个不同的盒中任取三个将球放入有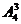 种方法,
种方法,
所以,一共有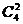
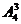 =144种方法.
=144种方法.
例4 马路上有编号为1,2,3,…,10的十盏路灯,为节约用电又不影响照明,可以把其中3盏灯关掉,但不可以同时关掉相邻的两盏或三盏,在两端的灯都不能关掉的情况下,有多少种不同的关灯方法?
解:(插空法)本题等价于在7只亮着的路灯之间的6个空档中插入3只熄掉的灯,
故所求方法总数为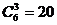 种方法。
种方法。
例5 九张卡片分别写着数字0,1,2,…,8,从中取出三张排成一排组成一个三位数,如果6可以当作9使用,问可以组成多少个三位数?
解:可以分为两类情况:① 若取出6,则有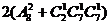 种方法;
种方法;
②若不取6,则有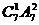 种方法,
种方法,
根据分类计数原理,一共有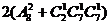 +
+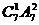 =602种方法。
=602种方法。
(一)复习、引入:
1.两个基本原理;
2.排列和组合的有关概念及相关性质。
2.提高合理选用知识解决问题的能力。
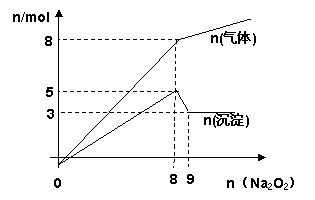
20.将Na2O2逐渐加入到2L含有Al3+、Mg2+、NH4+的混合液中并微热,产生沉淀和气体的物质的量(mol)
与加入Na2O2的物质的量(mol)的关系如图所示,则原混合溶液中Al3+、Mg2+、NH4+的物质的量浓度分别为多少?(不计溶液的体积变化)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com