13．若椭圆长轴长与短轴长之比为2，它的一个焦点是(2，0)，则椭圆的标准方程是__________．

解析：设椭圆标准方程为+＝1(a>b>0)，

由题意知＝2，即a＝2b，且c＝2，由a²＝b²+c²，解得

∴椭圆的标准方程为+＝1.

答案：+＝1

12．P为双曲线－＝1的右支上一点，M、N分别是圆(x+5)²+y²＝1和(x－5)²+y²＝4上的点，则|PM|－|PN|的最大值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．6　 　　　　　　　　　　　　　　　　　　　 B．7

C．8　 　　　　　　　　　　　　　　　　　　　 D．9

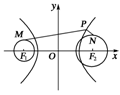
图3

解析：由于两圆心恰好为双曲线的焦点，

|PM|≤|PF₁|+r₁＝|PF₁|+1，

|PN|≥|PF₂|－r₂＝|PF₂|－2，

∴|PM|－|PN|

≤|PF₁|+1－(|PF₂|－2)

＝|PF₁|－|PF₂|+3＝2a+3＝9.

答案：D

11．设椭圆+＝1(a>b>0)的离心率e＝，右焦点为F(c,0)，方程ax²+bx－c＝0的两实根分别为x₁，x₂，则点P(x₁，x₂)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．必在圆x²+y²＝2内

B．必在圆x²+y²＝2上

C．必在圆x²+y²＝2外

D．以上情形都有可能

解析：∵e＝＝，∴a＝2c.

又∵a²＝b²+c²，∴b²＝a².

∵x₁+x₂＝－，x₁x₂＝，

∴x+x＝(x₁+x₂)²－2x₁x₂

＝+＝+2e＝+1＝<2.

答案：A

10．设O为坐标原点，F为抛物线y²＝4x的焦点，A为抛物线上一点，若·＝－4，则点A的坐标为　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．(2，±2)　 　　　　　　　　　　　　 B．(1，±2)

C．(1,2)　 　　　　　　　　　　　　　　　　 D．(2,2)

解析：设A(x₀，y₀)、F(1,0)，＝(x₀，y₀)，＝(1－x₀，－y₀)，·＝x₀(1－x₀)－y＝－4.

∵y＝4x₀，∴x₀－x－4x₀+4＝0⇒x+3x₀－4＝0，x₀＝1或x₀＝－4(舍去)．

∴x₀＝1，y₀＝±2.故选B.

答案：B

9．若抛物线y²＝2px的焦点与椭圆+＝1的右焦点重合，则p的值为　　　　 (　)

A．－2　 　　　　　　　　　　　　　　　　　 B．2

C．－4　 　　　　　　　　　　　　　　　　　 D．4

解析：椭圆的右焦点为F(2,0)，由题意＝2，

∴p＝4.

答案：D

8．若椭圆+＝1(a>b>0)的左、右焦点分别为F₁、F₂，线段F₁F₂被抛物线y²＝2bx的焦点分成5?3的两段，则此椭圆的离心率为　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　　　　　　　　　　 B.

C．2－　 　　　　　　　　　　　　　　　 D.

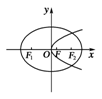
图2

解析：由已知|F₁F|?|FF₂|＝5?3，其中|F₂F|＝|OF₂|－|OF|＝c－，

|FF₁|＝|OF₁|+|OF|＝c+.

∴＝.∴c＝2b.

又∵a²＝b²+c²＝b²+4b²＝5b²，∴a＝b.

∴e＝＝＝.

答案：D

7．已知抛物线y²＝4x上的点P到抛物线的准线的距离为d₁，到直线3x－4y+9＝0的距离为d₂，则d₁+d₂的最小值是 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　　　　　　　　　　　　 B.

C．2　 　　　　　　　　　　　　　　　　　　　 D.

解析：根据抛物线的定义可知d₁等于点P到焦点的距离，故d₁+d₂的最小值即为抛物线上的点到焦点的距离和到直线的距离之和的最小值，易知当且仅当点P为过抛物线的焦点且与已知直线垂直的直线与抛物线的交点时，d₁+d₂最小．故(d₁+d₂)_min＝.

答案：A

6．(2010·吉林白山模拟)F₁，F₂是椭圆C：+＝1的两个焦点，在C上满足PF₁⊥PF₂的点P的个数为　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．0　 　　　　　　　　　　　　　　　　　　　 B．1

C．2　 　　　　　　　　　　　　　　　　　　　 D．4

解析：由+＝1，得a＝2，b＝2，c＝2.

∵b＝c＝2，∴以原点为圆心，c为半径的圆与椭圆有2个交点．

∴PF₁⊥PF₂的点P的个数为2.

答案：C

5．双曲线C和椭圆4x²+y²＝1有相同的焦点，它的一条渐近线为y＝x，则双曲线C的方程为　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．4x²－2y²＝1　 　　　　　　　　　　　 B．2x²－y²＝1

C．4x²－2y²＝－1　 　　　　　　　　　 D．2x²－y²＝－1

解析：设双曲线的方程为－＝1(a>0，b>0)双曲线的焦点坐标为(0，±)，又＝，

∴b＝，a＝.即双曲线方程为4x²－2y²＝－1，故选C.

答案：C

4．椭圆+＝1的左、右焦点是F₁、F₂，P是椭圆上一点，若|PF₁|＝3|PF₂|，则P点到左准线的距离是　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．2　 　　　　　　　　　　　　　　　　　　　 B．4

C．6　 　　　　　　　　　　　　　　　　　　　 D．8

解析：a＝＝2，b²＝3，c＝＝1.

因为|PF₁|+|PF₂|＝2a＝4，

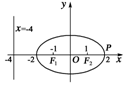
图1

|PF₁|＝3|PF₂|

所以|PF₂|＝1

如图1所示，P点是右顶点；

左准线x＝－＝－4，故P到左准线距离是：2－(－4)＝6.

答案：C