
21.(本小题满分15分)
已知椭圆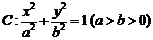 的离心率为
的离心率为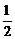 ,椭圆上的点到焦点的最小距离为1.
,椭圆上的点到焦点的最小距离为1.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若直线 与椭圆
与椭圆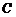 交于
交于 两点,且
两点,且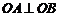 (
(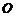 为坐标原点),
为坐标原点),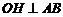 于
于 点.试求点
点.试求点 的轨迹方程.
的轨迹方程.
20. (本小题满分14分)
(本小题满分14分)
如图,在三棱柱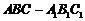 中,
中,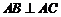 ,顶点
,顶点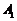 在
在
底面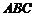 上的射影恰为B点,且
上的射影恰为B点,且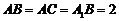 .
.
(Ⅰ)分别求出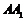 与底面
与底面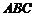 ,棱BC所成的角;
,棱BC所成的角;
(Ⅱ)在棱 上确定一点P,使
上确定一点P,使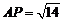 ,并求出
,并求出
二面角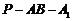 的平面角的余弦值.
的平面角的余弦值.
19.(本小题满分14分)
一袋子中有大小、质量均相同的10个小球,其中标记“开”字的小球有5个,标记“心”字的小球有3个,标记“乐”字的小球有2个.从中任意摸出1个球确定标记后放回袋中,再从中任取1个球.不断重复以上操作,最多取3次,并规定若取出“乐”字球,则停止摸球.求:
(Ⅰ)恰好摸到2个“心”字球的概率;
(Ⅱ)摸球次数 的概率分布列和数学期望.
的概率分布列和数学期望.
18.(本小题满分14分)
已知函数 .
.
(Ⅰ)求函数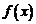 的单调递增区间;
的单调递增区间;
(Ⅱ)已知 ,且
,且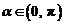 ,求
,求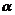 的值.
的值.
17.已知点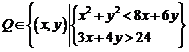 ,如果直线
,如果直线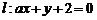 经过点
经过点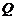 ,那么实数
,那么实数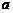 的取值范围是 ▲
.
的取值范围是 ▲
.
16.若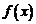 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当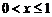 时,
时,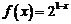 ;当
;当 时,
时,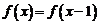 .则函数
.则函数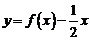 的零点有 ▲ 个.
的零点有 ▲ 个.
15.已知向量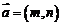 ,
,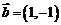 ,其中
,其中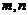 为连续两次投掷骰子得到的点数,则
为连续两次投掷骰子得到的点数,则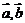 的夹角能成为直角三角形的内角的概率是 ▲
.
的夹角能成为直角三角形的内角的概率是 ▲
.
14.某个缺水地区为了提倡居民节约用水和控制用水浪费现象,实行了水费的分段计价,其计价的流程如图所示.其中输入为居民每月的用水量(单位:吨),输出为相应的水费(单位:元).已知某户居民某月用水量为 吨,则该户居民用水超过20吨的部分应缴纳的水费为 ▲
.
吨,则该户居民用水超过20吨的部分应缴纳的水费为 ▲
.
13.已知等差数列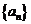 的前
的前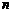 项和为
项和为 ,且过点
,且过点 和
和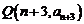
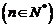 的直线的斜率是4,若
的直线的斜率是4,若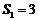 ,则
,则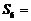 ▲ .
▲ .
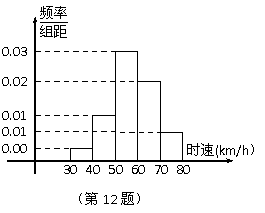
12.某路段属于限速路段,规定通过该路段的汽车时速不得超过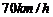 ,否则视为违规扣分.某天,有1000辆汽车经过了该路段,经过雷达测速得到这些汽车运行时速的频率分布直方图如图所示,则违规扣分的汽车大约为 ▲
辆.
,否则视为违规扣分.某天,有1000辆汽车经过了该路段,经过雷达测速得到这些汽车运行时速的频率分布直方图如图所示,则违规扣分的汽车大约为 ▲
辆.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com