
6.海滨浴场的滑梯从顶端到入水处长约12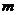 ,一个由滑梯顶端开始做初速度为零的匀加速直线运动,开始运动后第一秒通过路程是0.75
,一个由滑梯顶端开始做初速度为零的匀加速直线运动,开始运动后第一秒通过路程是0.75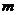 ,则人的加速度大小是 ,从顶端开始到入水,所需要的时间是
,人入水时的速度大小是 ,从顶端开始到入水人的平均速度的大小是 。
,则人的加速度大小是 ,从顶端开始到入水,所需要的时间是
,人入水时的速度大小是 ,从顶端开始到入水人的平均速度的大小是 。
5.两辆完全相同的汽车,沿水平直线一前一后匀速行驶,速度均为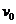 ,若前车突然以恒定加速度刹车,在它刚停车后,后车以与前车相同的加速度开始刹车,已知前车在刹车过程中所行的距离为
,若前车突然以恒定加速度刹车,在它刚停车后,后车以与前车相同的加速度开始刹车,已知前车在刹车过程中所行的距离为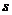 ,若要保证两车上述情况下不相撞,则两车在匀速行驶时应保持距离至少为( )
,若要保证两车上述情况下不相撞,则两车在匀速行驶时应保持距离至少为( )
A.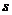 B.2
B.2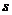 C.3
C.3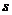 D.4
D.4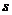
4.做匀变速直线运动的物体,在时间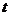 内的位移为
内的位移为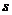 ,设这段时间中间时刻的瞬时速度为
,设这段时间中间时刻的瞬时速度为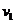 ,这段位移的中间位置的瞬时速度为
,这段位移的中间位置的瞬时速度为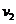 ,则( )
,则( )
A.无论是匀加速运动还是匀减速运动,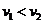
B.无论是匀加速运动还是匀减速运动,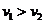
C.无论是匀加速运动还是匀减速运动,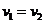
D.匀加速运动时,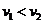 ,匀减速运动时,
,匀减速运动时,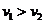
3.做匀加速直线运动的质点,运动了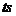 ,下列说法中正确的是( )
,下列说法中正确的是( )
A.它的初速度越大,通过的位移一定越大
B.它的加速度越大,通过的位移一定越大
C.它的末速度越大,通过的位移一定越大
D.它的平均速度越大,通过的位移一定越大
2.如图所示的是一质点做直线运动的速度-时间图像,则可知( )
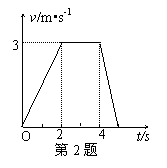 A.0-2s与4-5s内质点加速度方向相反
A.0-2s与4-5s内质点加速度方向相反
B.0-2s与4-5s内质点速度方向相反
C.2-4s内质点加速度最大
D.0-5s内的位移为10.5m
1.一个做匀加速直线运动的物体,初速度 ,它在第
,它在第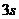 内通过的位移是
内通过的位移是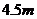 ,则它的加速度为( )
,则它的加速度为( )
A.0.5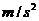 B.1.0
B.1.0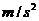 C.1.5
C.1.5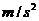 D.2.0
D.2.0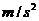
2.位移和速度的关系
我们知道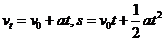
消去两式中的时间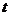 ,得到
,得到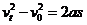
我们已知道两个位移公式: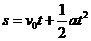 和
和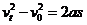
(1)以上两式仅适用于匀变速直线运动。
(2)解题时选择哪一个公式求解,要看已知量情况,因为前式中无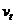 ,后式中无
,后式中无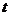 ,故选择公式时应尽量减少未知量。
,故选择公式时应尽量减少未知量。
(3)本节中所有公式皆为矢量式,除时间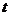 外,所有物理量皆为矢量,因此在解题时,要确定一个正方向,常选初速度方向为正方向,其余矢量依据其与
外,所有物理量皆为矢量,因此在解题时,要确定一个正方向,常选初速度方向为正方向,其余矢量依据其与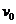 方向的关系(即相同或相反),分别代入“+”、“-”,如果某个量是待求的,可选假定其为“+”,最后根据结果的“+”、“-”确定实际方向。
方向的关系(即相同或相反),分别代入“+”、“-”,如果某个量是待求的,可选假定其为“+”,最后根据结果的“+”、“-”确定实际方向。
例6一个物体以初速度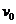 从斜面上滑下,滑到斜面底端时速度为
从斜面上滑下,滑到斜面底端时速度为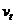 ,则它滑到斜面中点时速度是多大?
,则它滑到斜面中点时速度是多大?
解析:灵活应用不含时间的位移-速度关系即可求解。
设斜面长为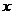 ,物体的加速度为
,物体的加速度为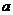 ,则有
,则有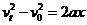
设滑到斜面中点时速度为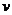 ,对前半程有
,对前半程有 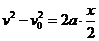
联立①、②得: 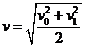
例7一个滑雪人,从85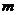 长的山坡上匀变速滑下,初速度是1.8
长的山坡上匀变速滑下,初速度是1.8 ,末速度是5.0
,末速度是5.0 。他通过这段山坡需要多长时间?
。他通过这段山坡需要多长时间?
解析:滑雪人的运动可以看作是匀加速直线运动,可以利用匀变速直线运动的规律来求,已知量的初速度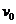 ,末速度
,末速度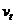 和位移
和位移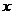 ,待求量是时间
,待求量是时间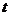 ,我们可以用不同的方法求解。
,我们可以用不同的方法求解。
解法I:利用公式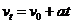 和
和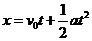 求解。
求解。
由公式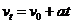 得,需要的时间
得,需要的时间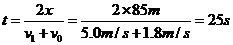
解法Ⅱ:利用公式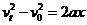 和
和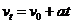 求解,由公式
求解,由公式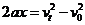 得,加速度
得,加速度
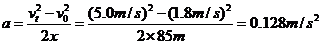
由公式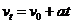 得,需要的时间
得,需要的时间

解法Ⅲ:利用平均速度的公式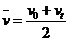 和
和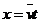 求解
求解
平均速度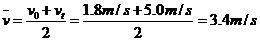
由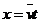 得,需要的时间
得,需要的时间 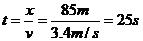
[同步检测]
1.匀变速直线运动的位移公式
根据平均速度的定义式,做任何变速运动的位移都可以表示为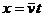 ,则匀变速直线运动的位移公式为
,则匀变速直线运动的位移公式为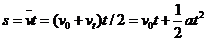
(1)位移公式说明匀变速直线运动的位移与时间是二次函数关系,式中的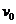 是初速度,时间
是初速度,时间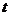 应是物体实际运动的时间。
应是物体实际运动的时间。
(2)在取初速度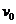 方向为正方向的前提下,匀加速度直线运动
方向为正方向的前提下,匀加速度直线运动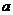 取正值,匀减速直线运动
取正值,匀减速直线运动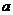 取负值;计算的结果
取负值;计算的结果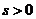 ,说明位移的方向与初速度的方向相同;
,说明位移的方向与初速度的方向相同;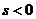 说明位移的方向与初速度的方向相反。
说明位移的方向与初速度的方向相反。
(3)对于初速度为零(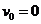 )的匀变速直线运动,位移公式为
)的匀变速直线运动,位移公式为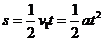
即位移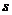 与时间
与时间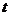 的二次方成正比。
的二次方成正比。
(4)速度-时间图像下的面积表示位移的大小,且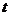 轴上方的面积表示正位移,
轴上方的面积表示正位移,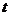 轴下方的面积表示负位移。
轴下方的面积表示负位移。
例1某做直线运动的质点的位移随时间变化的关系式为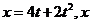 与
与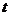 的单位分别是
的单位分别是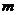 和
和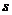 ,则质点的初速度和加速度分别是( )
,则质点的初速度和加速度分别是( )
A.4 和2
和2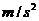 B.0和4
B.0和4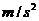
C.4 和4
和4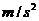 D.4
D.4 和0
和0
解析:做匀加速直线运动的位移随时间变化的关系式为:X =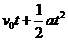 ,与关系式
,与关系式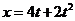 相比较,
相比较,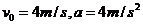 ,所以只有C正确。
,所以只有C正确。
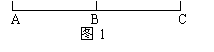 例2一辆汽车在笔直的公路上做匀变速直线运动,该公路每隔15
例2一辆汽车在笔直的公路上做匀变速直线运动,该公路每隔15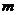 安置一个路标,如图1所示,汽车通过AB两相邻路标用了2
安置一个路标,如图1所示,汽车通过AB两相邻路标用了2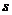 ,通过BC两路标用了3
,通过BC两路标用了3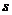 ,求汽车通过A、B、C三个路标时的速度。
,求汽车通过A、B、C三个路标时的速度。
解析:汽车从A到C是匀减速运动,设汽车通过路标A时速度为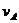 ,通过AB的时间
,通过AB的时间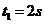 ,通过BC的时间
,通过BC的时间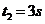 。
。
根据位移公式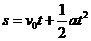 ,研究AB运动的过程,
,研究AB运动的过程,
有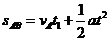 ,研究AC运动过程,有
,研究AC运动过程,有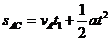
其中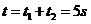
解得:
再根据速度公式
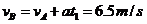
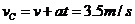
例3 以18 的速度行驶的汽车,紧急刹车后做匀减速直线运动,其加速度大小为6
的速度行驶的汽车,紧急刹车后做匀减速直线运动,其加速度大小为6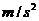 ,求:
,求:
(1)汽车在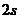 内通过的距离;
内通过的距离;
(2)汽车在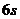 内通过的距离。
内通过的距离。
解析:应首先判断所求位移对应的时间内汽车是否一直在运动,然后利用匀变速直线运动的位移公式进行求解。
已知汽车刹车时间的初速度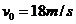 ,因为是匀减速直线运动,所以加速度
,因为是匀减速直线运动,所以加速度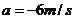 ,设经过
,设经过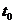 秒汽车停止运动
秒汽车停止运动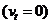 ,则由
,则由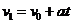
得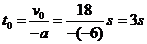
因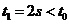 ,故前
,故前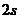 内汽车一直在运动,所以前
内汽车一直在运动,所以前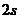 内通过的距离(即位移的大小)
内通过的距离(即位移的大小)
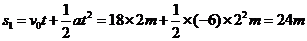
又因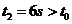 ,汽车刹车后运动
,汽车刹车后运动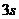 就停下来了,所以
就停下来了,所以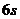 内汽车通过的距离也就是
内汽车通过的距离也就是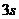 内汽车通过的距离,所以
内汽车通过的距离,所以 内汽车通过的距离为
内汽车通过的距离为
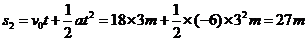
[规律总结]对于匀减速直线运动,一定要注意速度减为零后是静止不动还是又反向加速了。对于汽车刹车、飞机着陆等依靠运动阻力减速的物体来说,速度减为零后即静止。所以必须选判定运动物体所经历的实际时间,然后再根据具体条件进行求解。
例4有一个做匀变速直线运动的质点,它在两段连续相等时间内通过的位移分别是24m和64m,连续相等的时间为4s,求质点的初速度和加速度的大小。
解析:根据位移公式得
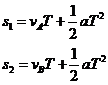
根据速度公式得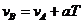
将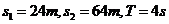 代入上面三式,联立解得
代入上面三式,联立解得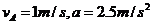
[规律总结]匀变速运动的每一个公式都涉及四个物理量,解题时应注意根据题目所给的三个已知量,以及要求的未知量,合理选用公式。
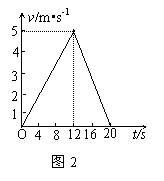 例5从车站开出的汽车,做匀加速运动,走了12s时,发现还有乘客没上来,于是立即做匀减速运动至停车,总共历时20s,行进了50m,求汽车的最大速度。
例5从车站开出的汽车,做匀加速运动,走了12s时,发现还有乘客没上来,于是立即做匀减速运动至停车,总共历时20s,行进了50m,求汽车的最大速度。
解析:汽车先做初速度为零的匀加速直线运动,达到最高速度后,立即改做匀减速运动,可以应用解析法,也可应用图象法。
设最高速度为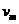 ,由题意,可得方程组
,由题意,可得方程组

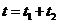
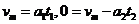
整理得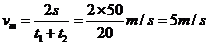
应用图像法,作出运动全过程的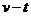 图像如图所示,
图像如图所示,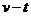 图线与
图线与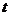 轴围成三角形的面积与位移等值,故
轴围成三角形的面积与位移等值,故
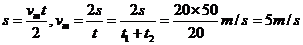
[规律总结]解决运动学问题的关键是理解运动过程,画出运动过程的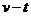 图,再选择恰当的公式求解。
图,再选择恰当的公式求解。
4.由匀变速直线运动的速度-时间公式和位移-时间公式可以推出速度-位移公式是
,若初速度为零,则位移公式是 ,速度-位移公式是 。
[同步导学]
3.匀变速直线运动的位移公式是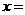 ,其中是矢量的物理量有
,是标量的物理量有
。
,其中是矢量的物理量有
,是标量的物理量有
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com