
4. 在等差数列{an}与等比数列{bn}中,a1=b1>0,a2n+1=b2n+1>0(n=1,2,3,…),则an+1与bn+1的大小关系是____________.
3. (2005春北京)若不等式(-1)na<2+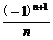 对任意n∈N*恒成立,则实数a的取值范围是 ( )
对任意n∈N*恒成立,则实数a的取值范围是 ( )
A.[-2, ) B.(-2,
) B.(-2, )
)
C.[-3, ) D.(-3,
) D.(-3, )
)
2. 设M=a+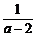 (2<a<3),N=log
(2<a<3),N=log (x2+
(x2+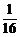 )(x∈R),那么M、N的大小关系是
)(x∈R),那么M、N的大小关系是
A.M>N B.M=N C.M<N D.不能确定
1. 已知a、b是不相等的正数,x= ,y=
,y=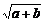 ,则x、y的关系是( )
,则x、y的关系是( )
A.x>y B.y>x C.x>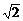 y D.不能确定
y D.不能确定
6.利用函数的单调性.利用单调函数中自变量大小与函数值之间的联系.要特别重视这种方法,因为高考中常把不等式综合在函数、数列或其它数学问题之中。
5.数学归纳法法:证明与正整数有关的不等式
4.构造法:通过构造函数、方程或几何图形,利用相关知识来证明不等式;
1.反证法:正难则反. 否定结论,导出矛盾,证实结论的否定是错误的,从而肯定原结论正确。
2.放缩法:将不等式一侧适当的放大或缩小,利用不等式的传递性证 明不等式.
常用的放缩手法有:
①添加或舍去一些项,如: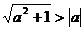 ;
;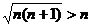 ;
;
②将分子或分母放大(或缩小)
③利用基本不等式,绝对值不等式,a2≥0等;
④若a>b>0,m>0,则 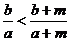 .
.
3.换元法:换元的目的是减少不等式中的变量,或者化繁为简.常用的换元有三角换元和代数换元.换元法必须注意新变元的取值范围.
2.了解换元法、判别式法、数形结合、构造法,了解不等式证明方法的多样性和灵活性.提高分析问题,解决问题的能力.
1.掌握反证法、数学归纳法和放缩法的一些策略技巧;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com