
9.解不等式: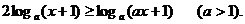
解:原不等式
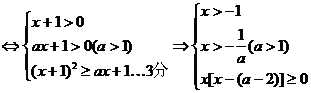
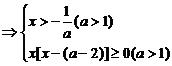
①∴a=2时,不等式的角为x>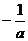 ;
;
②a>2时,a-2>0, 故原不等式解为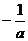 <x≤0或x≥a-2
<x≤0或x≥a-2
③当1<a<2时,a-2<0,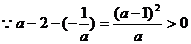
∴原不等式解为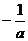 <x≤a-2或x≥0
<x≤a-2或x≥0
8. 己知三个不等式:①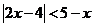
 ②
②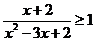 ③
③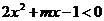
(1)若同时满足①、②的 值也满足③,求m的取值范围;
值也满足③,求m的取值范围;
(2)若满足③的 值至少满足①和②中的一个,求m的取值范围。
值至少满足①和②中的一个,求m的取值范围。
分析:本例主要综合复习整式、分式不等式和含绝对值不等式的解法,以及数形结合思想,解本题的关键弄清同时满足①、②的 值的满足③的充要条件是:③对应的方程的两根分别在
值的满足③的充要条件是:③对应的方程的两根分别在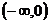 和
和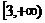 内。不等式和与之对应的方程及函数图象有着密不可分的内在联系,在解决问题的过程中,要适时地联系它们之间的内在关系。
内。不等式和与之对应的方程及函数图象有着密不可分的内在联系,在解决问题的过程中,要适时地联系它们之间的内在关系。
解:记①的解集为A,②的解集为B,③的解集为C。
解①得A=(-1,3);解②得B=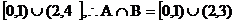
(1) 因同时满足①、②的 值也满足③,A
值也满足③,A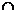 B
B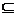 C
C
设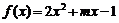 ,由
,由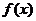 的图象可知:方程的小根小于0,大根大于或等于3时,即可满足
的图象可知:方程的小根小于0,大根大于或等于3时,即可满足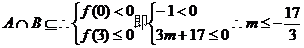
(2) 因满足③的 值至少满足①和②中的一个,
值至少满足①和②中的一个,
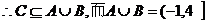 , 因此
, 因此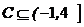
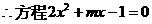 小根大于或等于-1,大根小于或等于4,因而
小根大于或等于-1,大根小于或等于4,因而
说明:同时满足①②的x值满足③的充要条件是:③对应的方程2x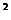 +mx-1=0的两根分别在(-∞,0)和[3,+∞)内,因此有f(0)<0且f(3)≤0,否则不能对A∩B中的所有x值满足条件.不等式和与之对应的方程及图象是有着密不可分的内在联系的,在解决问题的过程中,要适时地联系它们之间的内在关系.
+mx-1=0的两根分别在(-∞,0)和[3,+∞)内,因此有f(0)<0且f(3)≤0,否则不能对A∩B中的所有x值满足条件.不等式和与之对应的方程及图象是有着密不可分的内在联系的,在解决问题的过程中,要适时地联系它们之间的内在关系.
7.解不等式:(1)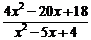 >3.
>3.
(2)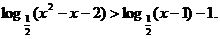
解(1)原不等式可化为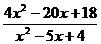 -3>0
-3>0

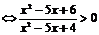
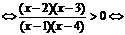
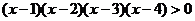
标根作图如下:
∴x∈(-∞,1)∪(2,3)∪(4,+∞).
(2)原不等式变形为
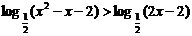 .
.
∴原不等式
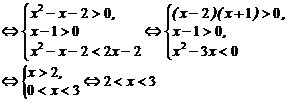 .
.
故原不等式的解集为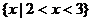
6.由已知a<0,α、β为方程ax2+bx+c=0的两根,
∴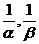 是方程cx2+bx+a=0的根,且
是方程cx2+bx+a=0的根,且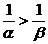
由韦达定理: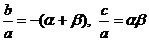 ,
,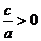 ,a<0得c<0,
,a<0得c<0,
∴不等式cx2+bx+a<0的解集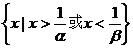 .
.
[解答题]
6.不等式ax2+bx+c>0的解集为{x|α<x<β}其中β>α>0,则不等式cx2+bx+a<0的解集是_____________。
简答.提示:1-3.ACC; 4. 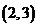 ; 5. 155;
; 5. 155;
5.
(2005全国Ⅰ) 若正整数m满足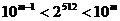 ,则m =
,则m = 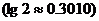
4. (2006重庆)设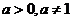 ,函数
,函数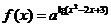 有最大值,则不等式
有最大值,则不等式
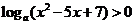 的解集为 。
的解集为 。
3.(2005辽宁)若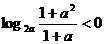 ,则
,则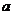 的取值范围是( )
的取值范围是( )
A.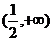 B.
B.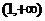 C.
C.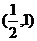 D.
D.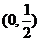
[填空题]
2.(2006江西6)若不等式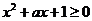 对一切
对一切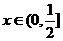 成立,则
成立,则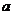 的最小值为( )
的最小值为( )
A.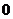 B.
B.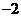 C.
C.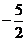 D.
D. 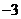
1.(2004年天津卷)不等式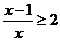 的解集为 ( )
的解集为 ( )
A.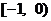 B.
B.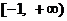 C.
C.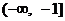 D.
D.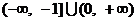
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com