
6.影响我国的台风主要形成于图一中的
A.① B.② C.③ D.④
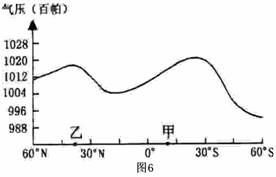
5.该月份乙地的气候特征是:
A.高温多雨 B.低温少雨
C.温和多雨 D.炎热干燥
我国是世界上受台风影响最大的国家之一,2008年7月29日,强台风“凤凰”在福建省再次登陆,造成严重危害。图一为“北半球易形成台风海区分布示意图”;图二为福建某城市在此次台风天气过程中的风向和风力变化图。风杆(长线段)上绘有风尾(短线段)的一方指示风向。每一道风尾表示风力2级,一个风旗表示风力8-12级。读图,回答6-7题。

4.该月份甲地盛行:
A.东南风 B.东北风
C.西南风 D.西北风
3. 上述“某月”是:
上述“某月”是:
A.1月 B.4月
C.7月 D.10月
2.该月份甲地盛行风向及气候特征分别是
A.东南风 B.东北风 C.西南风 D.西北风
图6为“某月沿0°经线海平面平均气压分布图”。读图回答3-5题。
1.上述“某月”是
A.1月 B.4月 C.7月 D.10月
9. 已知两点A(2,3)、B(4,1),直线l:x+2y-2=0,在直线l上求一点P.
(1)使|PA|+|PB|最小;
(2)使|PA|-|PB|最大.
解:(1)可判断A、B在直线l的同侧,设A点关于l的对称点A1的坐标为(x1,y1).
|

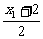 +2·
+2· -2=0,
-2=0,
 ·(-
·(- )=-1.
)=-1.
|
 x1=-
x1=- ,
,
y1=- .
.
由两点式求得直线A1B的方程为y=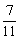 (x-4)+1,直线A1B与l的交点可求得为P(
(x-4)+1,直线A1B与l的交点可求得为P( ,-
,- ).
).
由平面几何知识可知|PA|+|PB|最小.
(2)由两点式求得直线AB的方程为y-1=-(x-4),即x+y-5=0.
直线AB与l的交点可求得为P(8,-3),它使|PA|-|PB|最大.
10若抛物线y=2x2上的两点A(x1,y1)、B(x2,y2)关于直线y=x+m对称且x1x2=- ,求m的值
,求m的值
解:设直线AB的方程为y=-x+b,代入y=2x2得2x2+x-b=0,
∴x1+x2=- ,x1x2=
,x1x2=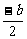 =-
=-
 ∴b=1,即AB的方程为y=-x+1
∴b=1,即AB的方程为y=-x+1
设AB的中点为M(x0,y0),则x0= =-
=- ,代入y0=-x0+1,
,代入y0=-x0+1,
得y0=
 又M(-
又M(- ,
, )在y=x+m上,∴
)在y=x+m上,∴ =-
=- +m
+m ∴m=
∴m=
[探索题]已知椭圆方程为 ,试确定实数
,试确定实数 的取值范围,使得椭圆上有不同的两点关于直线
的取值范围,使得椭圆上有不同的两点关于直线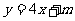 对称。
对称。
解法一:该
问题等价于存在直线 ,使得这直线与椭圆有两个不同的交点
,使得这直线与椭圆有两个不同的交点 、
、 ,线段
,线段 的中点落在直线
的中点落在直线
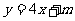 上。
上。
由 消去y得
消去y得
∵直线与椭圆有两个不同交点。
 ∴
∴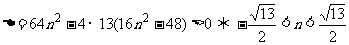 ①
①
由韦达定理得: ,
, 。
。
故 中点为
中点为 又
又 在直线
在直线
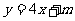 上
上
∴ ,∴
,∴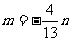 ②
②
由①②知
解法二:设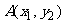 、
、 是椭圆上关于直线
是椭圆上关于直线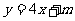 对称的相异的两点,
对称的相异的两点,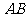 中点为
中点为 。则
。则 ,
, ,
,
由点差法得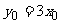 ,代入
,代入 解得,
解得, 点坐标为
点坐标为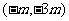 。
。
而 是
是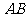 中点,∴
中点,∴ 点在椭圆内部。
点在椭圆内部。
∴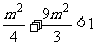 。解得
。解得 。
。
8. 已知△ABC的一个顶点A(-1,-4),∠B、∠C的平分线所在直线的方程分别为l1:y+1=0,l2:x+y+1=0,求边BC所在直线的方程.
解:设点A(-1,-4)关于直线y+1=0的对称点为A′(x1,y1),则x1=-1,y1=2×(-1)-(-4)=2,即A′(-1,2).
在直线BC上,再设点A(-1,-4)关于l2:x+y+1=0的对称点为A″(x2,y2),则有

 ×(-1)=-1,
×(-1)=-1,
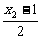 +
+ +1=0.
+1=0.
|
 x2=3,
x2=3,
y2=0,
即A″(3,0)也在直线BC上,由直线方程的两点式得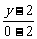 =
= ,即x+2y-3=0为边BC所在直线的方程.
,即x+2y-3=0为边BC所在直线的方程.
7.一条光线经过P(2,3)点,射在直线 :x+y+1=0上,反射后穿过点Q(1,1)
:x+y+1=0上,反射后穿过点Q(1,1)
(1) 求入射光线所在的直线方程
(2) 求这条光线从P到Q的长度。
解:(1)设Q(1,1)关于:x+y+1=0的对称点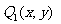 ,易证
,易证
入射光线所在直线方程 ,即5x-4y+2=0
,即5x-4y+2=0
(2) 是
是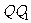 的垂直平分线,因而
的垂直平分线,因而 即为所求
即为所求
6.答案:1/3, 5说明:掌握k=±1时,求对称点的方法
[解答题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com