1．What did the man do yester day?

　　 A．He had a rest.

　　 B．He looked for jobs.

　　 C．He took some exams.

20．(本题满分13分)

　　　　 已知函数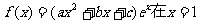处取得极小值，其图象过点A(0，1)，且在点A处切线的斜率为-1。

　 (1)求的解析式；

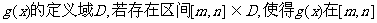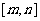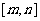　 (2)设函数上的值域也是，则称区间为函数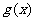的“保值区间”。

　　　　 ①证明：当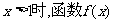不存在“保值区间”；

②函数是否存在“保值区间”？若存在，写出一个“保值区间”(不必证明)；若不存在，说明理由。

19．(本题满分12分)

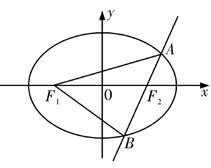
　　 已知椭圆C的中心在原点，焦点F₁，F₂在x轴上，离心率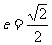，且经过点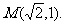

　 (1)求椭圆C的方程；

　 (2)若直线l经过椭圆C的右焦点F₂，且与椭圆C交于A，B两点，使得|F₁A|，|AB|，|BF₁|依次成等差数列，求直线l的方程。

18．(本题满分10分)

　　 已知数列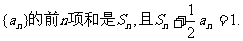

　 (1)求数列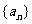的通项公式；

　 (2)设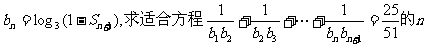的值。

17．(本题满分10分)

甲，乙两人进行射击比赛，每人射击6次，他们命中的环数如下表：

　 (1)根据上表中的数据,判断甲,乙两人谁发挥较稳定；

　 (2)把甲6次射击命中的环数看成一个总体,用简单随机抽样方法从中抽取两次命中的环数组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过0.5的概率.

16．(本题满分10分)

已知向量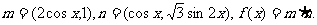

　 (1)求的最小正周期和最大值；

　 (2)在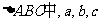分别是角A、B、C的对边，且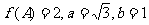，求角C。

15．将所有3的幂，或者是若干个不相等的3的幂之和，

由小到大依次排列成数列1，3，4，9，10，12，13，…,则此数列的第100项为　　　 .

14．已知圆C的极坐标方程为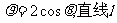的极坐标

方程为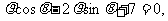则圆心C到直线l的

距离是　　　　　　 。

13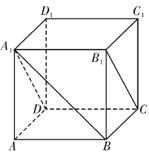．如图，在正方体ABCD-A₁B₁C₁D₁中，直线A₁B

与平面A₁B₁CD 所成的角的大小等于　　　　 .

12．在区间[1，9]上随机取一实数，则该实数在区间[4，7]上的概率为　　　　　 .