
⑴定义:由烃基或H与羧基相连的一类化合物,官能团为 -COOH
⑵分类:
 C原子数目:低级,高级脂肪酸
C原子数目:低级,高级脂肪酸
 脂肪酸
脂肪酸
 烃基种类
烃基的饱和情况:饱和,不饱和
烃基种类
烃基的饱和情况:饱和,不饱和
|
 一元羧酸
一元羧酸
羧基数目
多元羧酸
⑶饱和一元羧酸:CnH2nO2
①酸CnH2nO2的同分异构体的数目:看R-COOH中-R的异构体数目
②与C数相同的饱和一元酯异构
⑷物性:①熔沸点:随n↑而升高
②溶解性:随n↑而减小(低级脂肪酸易溶,高级脂肪酸不溶)
2.物理性质:
乙酸俗称 ,它是一种无色 气味的 体,易挥发,熔、沸点较 ,其熔点为16.6℃时,因此当温度低于16.6℃时,乙酸就凝成像冰一样的晶体,故无水乙酸又称 。它易溶于水和乙醚等溶剂。
⒊化学性质:
⑴酸性:CH3COOH>H2CO3>C6H5OH
设计一个简单的一次性完成的实验装置,验证乙酸、碳酸和苯酚溶液的酸性强弱。
⑵酯化反应:CH3COOH+C2H5OH CH3COO
C2H5+H2O
CH3COO
C2H5+H2O
思考:你能设计实验方案证明酯化反应的脱水方式吗?
①试剂加入顺序:
②加热目的:
③饱和Na2CO3的作用:
④现象:
1.结构:分子式 最简式 结构简式:
2.(10分)“细菌冶金”是利用某些细菌的特殊代谢功能开采金属矿石,例如溶液中氧化亚铁硫杆菌能利用空气中的氧气将黄铁矿(主要成分FeS2)氧化为Fe2(SO4)3,并使溶液酸性增强,其过程如图:
 ⑴ 该过程的化学反应方程式为
。
⑴ 该过程的化学反应方程式为
。
⑵ 人们可利用Fe2(SO4)3作强氧化剂溶解铜矿石(Cu2S),然后加入铁屑进一步得到铜,该过程中发生的离子反应方程式(请将①补充完整):
① Cu2S+ Fe3++
H2O Cu2++
Fe2++
( )+ SO42-
Cu2++
Fe2++
( )+ SO42-
② 。
⑶ 工业上可利用粗铜(含Zn、Ag、Au杂质)经电解制得精铜(电解铜)。则阳极和阴极材料分别为: 和 ,阳极的电极反应式为 , 。
⑷ 请评价细菌冶金的优点 。(说一点即可)
1.(12分)工业上以黄铁矿为原料生产硫酸主要分为三个阶段进行,即在沸腾炉中煅烧黄铁矿、SO2的催化氧化及其SO3的吸收。请回答下列几个有关硫酸工业中的几个问题。
(1)从沸腾炉中出来的炉气必须经除尘、洗涤、干燥后进入接触室,其主要目的是_____________。
(2)接触室中热交换器是实现冷热交换的装置。化学实验中也经常利用热交换来实现某种实验目的,如气、液热交换时通常使用的仪器是______________。
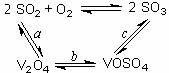 (3)接触室中主要反应是SO2的催化氧化,在生成硫酸的过程中,钒触媒(V2O5)所以能加快二氧化硫氧化的速度,除了具有吸附作用外,有人认为反应过程中还产生了一连串的中间体(如图)。a、c二步的化学方程式可表示为_______________________、__________________。反应b的原子利用率为_________。
(3)接触室中主要反应是SO2的催化氧化,在生成硫酸的过程中,钒触媒(V2O5)所以能加快二氧化硫氧化的速度,除了具有吸附作用外,有人认为反应过程中还产生了一连串的中间体(如图)。a、c二步的化学方程式可表示为_______________________、__________________。反应b的原子利用率为_________。
(4) 工业上以硫铁矿为原料制硫酸所产生的尾气除了
含有N2、O2外,还含有SO2、微量的SO3和酸雾。为了保护环境,同时提高硫酸工业的综合经济效益,应尽可能将尾气中的SO2转化为有用的副产品。将尾气通入粉末状的碳酸钙或熟石灰的悬浊液中,经过一系列处理后得到一种相对分子质量为172的化工原料J。试写出J的化学式_________。
解:(1)点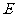 在
在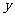 轴上································································································· 1分
轴上································································································· 1分
理由如下:连接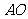 ,如图所示,在
,如图所示,在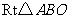 中,
中,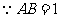 ,
,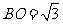 ,
,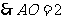
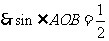 ,
,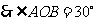
由题意可知: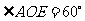
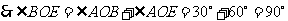
 点
点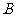 在
在 轴上,
轴上,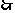 点
点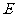 在
在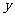 轴上.············································································ 2分
轴上.············································································ 2分
(2)过点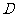 作
作 轴于点
轴于点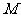
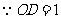 ,
,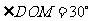
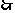 在
在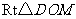 中,
中,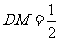 ,
,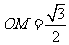
 点
点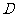 在第一象限,
在第一象限,
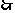 点
点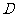 的坐标为
的坐标为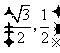 ····························································································· 4分
····························································································· 4分
由(1)知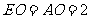 ,点
,点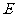 在
在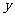 轴的正半轴上
轴的正半轴上
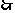 点
点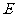 的坐标为
的坐标为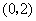
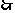 点
点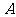 的坐标为
的坐标为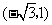 ······························································································· 5分
······························································································· 5分
 抛物线
抛物线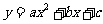 经过点
经过点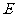 ,
, 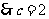
由题意,将 ,
,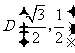 代入
代入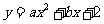 中得
中得
 解得
解得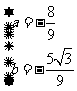
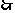 所求抛物线表达式为:
所求抛物线表达式为: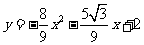 ·························································· 7分
·························································· 7分
(3)存在符合条件的点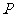 ,点
,点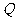 .·············································································· 8分
.·············································································· 8分
理由如下: 矩形
矩形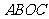 的面积
的面积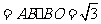
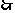 以
以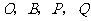 为顶点的平行四边形面积为
为顶点的平行四边形面积为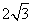 .
.
由题意可知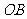 为此平行四边形一边,
又
为此平行四边形一边,
又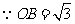
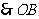 边上的高为2······································································································ 10分
边上的高为2······································································································ 10分
依题意设点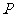 的坐标为
的坐标为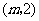
 点
点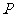 在抛物线
在抛物线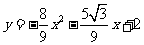 上
上
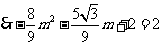
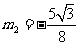
解得,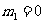 ,
,
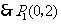 ,
,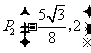
 以
以 为顶点的四边形是平行四边形,
为顶点的四边形是平行四边形,
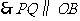 ,
,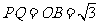 ,
,
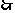 当点
当点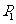 的坐标为
的坐标为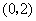 时,
时,
点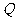 的坐标分别为
的坐标分别为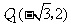 ,
,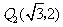 ;
;
当点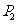 的坐标为
的坐标为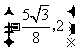 时,
时,
点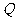 的坐标分别为
的坐标分别为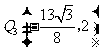 ,
,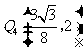 .·················································· 12分
.·················································· 12分
15. 33
16. 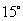 17.
17. 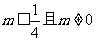 18. 4 19. 4 20. 0 21. 1 22. 14
18. 4 19. 4 20. 0 21. 1 22. 14
7. -1
8. 195 9. 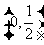 10. 3或-3
11.
10. 3或-3
11. 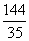 12. 3 13.
12. 3 13.  14.
14. 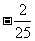
1. D 2. B 3. B 4. B 5. C 6. C
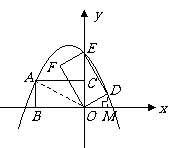
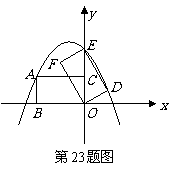
23. 如图所示,在平面直角坐标系中,矩形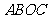 的边
的边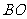 在
在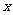 轴的负半轴上,边
轴的负半轴上,边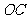 在
在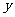 轴的正半轴上,且
轴的正半轴上,且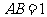 ,
,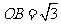 ,矩形
,矩形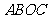 绕点
绕点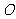 按顺时针方向旋转
按顺时针方向旋转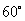 后得到矩形
后得到矩形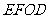 .点
.点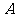 的对应点为点
的对应点为点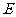 ,点
,点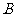 的对应点为点
的对应点为点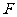 ,点
,点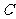 的对应点为点
的对应点为点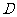 ,抛物线
,抛物线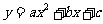 过点
过点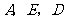 .
.
(1)判断点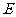 是否在
是否在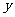 轴上,并说明理由;
轴上,并说明理由;
(2)求抛物线的函数表达式;
(3)在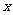 轴的上方是否存在点
轴的上方是否存在点 ,点
,点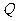 ,使以点
,使以点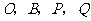 为顶点的平行四边形的面积是矩形
为顶点的平行四边形的面积是矩形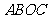 面积的2倍,且点
面积的2倍,且点 在抛物线上,若存在,请求出点
在抛物线上,若存在,请求出点 ,点
,点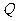 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com