5.(2006辽宁)5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员排成1、2、3号参加团体比赛,则入选的3名队员中至少有一名老队员,且1、2号中至少有1名新队员的排法有_____种.(以数作答)

4.(2005辽宁)用1、2、3、4、5、6、7、8组成没有重复数字的八位数，要求1和2相邻，3与4相邻，5与6相邻，而7与8不相邻，这样的八位数共有　　　　　 个.(用数字作答)

3.某年级有6个班，派3个数学老师任教，每位教师教两个班，不同的任课方法种数有_______种.

2.(2005湖南)4位同学参加某种形式的竞赛，竞赛规则规定：每位同学必须从甲．乙两道题中任选一题作答，选甲题答对得100分，答错得－100分；选乙题答对得90分，答错得－90分.若4位同学的总分为0，则这4位同学不同得分情况的种数是(　 )

　A．48　　　　　 B．36　　　　　　　　　 C．24　　　　　　　　 D．18

[填空题]

1.(2006天津)将4个颜色互不相同的球全部放入编号为1和2的两个盒子里，使得放入每个盒子里的球的个数不小于该盒子的编号，则不同的放球方法有(　)

A．10种　　　　　　　 B．20种　　　　　　　 C．36种　　　　　　　 D．52种

3. 记住一些常题型的特殊解法;如捆绑法,插空法, 排除法, 插板法,分组、分配等.

同步练习　 　　　10.3排列组全的综合应用　

[选择题]

2.对于有附加条件的排列组合应用题，应掌握以下基本方法与技巧

(1)特殊元素优先安排；(2)合理分类与准确分步；(3)先选后排；(4)相邻问题捆绑处理；(5)不相邻问题插空处理；(6)定序问题排除法处理；(7)分排问题直排处理；(8)“小集团”排列问题先整体后局部；(9)构造模型；(10)正难则反，等价转化.

1.对排列、组合的应用题应遵循两个原则：一是按元素的性质进行分类；二是按事件发生的过程进行分步.

[例1]设有编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的五个盒子，现将这五个球放入5个盒子内

(1)只有一个盒子空着，共有多少种投放方法？

(2)没有一个盒子空着，但球的编号与盒子编号不全相同，有多少种投放方法？

(3)每个盒子内投放一球，并且至少有两个球的编号与盒子编号是相同的，有多少种投放方法？

解:(1)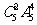 =1200(种)　　　　 (2)-1=119(种)　　　　　　　　　　

(3)不满足的情形：第一类，恰有一球相同的放法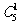：×9=45

第二类，五个球的编号与盒子编号全不同的放法：

　 先让1号球放，1号球放到哪个盒中就让哪个球放，……

有 4×(2+3×3)=44 (种) , ∴ 满足条件的放法数为：-45-44=31(种)

　 [例2]某运输公司有3个车队,每个车队有10辆汽车, 现从这3个车队中选派6辆汽车执行一项运输任务,每个车队至少1辆共有多少种选派方法?

　 分析：这里所谓不同的选派方法，只是每个车队派车数目的不同，是相同元素的分组问题--用“插板法”

　 解：把6个派车指标排成一排，是一种排法，有5个空，插2个板，分成3组即可，共有　　 =10(种)

◆拓展引伸：方程x+y+z=7有多少组正整数解？(看成7个相同的元素分给3人)

　 若求方程x+y+z=7有多少组自然数解呢？(让3人每人拿出1个元素，如上法分10个元素)

[例3]某学习小组有8名同学,从男生中选2人,女生中选1人参加数学、物理、化学三种竞赛，要求每科均有一人参加，共有180种不同的选法，那么该小组中共有男女同学多少人？

解：设有男生n人，女生8-n人，则有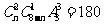即(n-1)n(8-n)=60.

又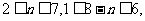

60的小于等于7的因数有1、2、3、4、5、6，因为n-1和n相邻，

∴n=5,8-n=3,即男生5人，女生3人，或n=6,8-n=2，即男生6人，女生2人。

◆　 提炼方法：1.引进待定的未知数,列方程求解;

2.“先取元素，后排顺序”.一类重要题型和方法。

[例4]一栋7层的楼房备有电梯,现有A,B,C,D,E五人从一楼进电梯上楼，求

(1)有且仅有一人要上7楼，且甲不在2楼下电梯的所有可能情况种数.

(2)在(1)的条件下,一层只能下1个人,共有多少种情况?

解: (1)分A上不上7楼两类：

　A上7楼，有5⁴种； A不上7楼，有4×4×4³种.

共有5⁴+4×4×4³＝1649种．

(2)分2楼下人和不下人两类,每类再分A上不上7楼两种情况.

2楼下人,有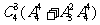种;　 2楼不下人,有种

∴共有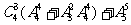 =504种情况.

◆提炼方法：题(1)是计数原理,题(2)是排列组合,应注意区分.

[研讨.欣赏](1)一条长椅上有9个座位，3个人坐，若相邻2人之间至少有2个空椅子，共有几种不同的坐法?

(2)一条长椅上有7个座位，4个人坐，要求3个空位中，恰有2个空位相邻，共有多少种不同的坐法?

解：(1)先将3人(用×表示)与4张空椅子(用□表示)排列如图(×□□×□□×)，这时共占据了7张椅子，还有2张空椅子，一是分开插入，如图中箭头所示(↓×□↓□×□↓□×↓)，从4个空当中选2个插入，有C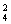种插法；二是2张同时插入，有C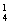种插法，再考虑3人可交换有A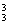种方法.

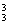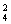所以，共有A(C+C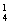)=60(种).

下面再看另一种构造方法：

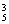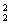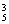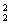先将3人与2张空椅子排成一排，从5个位置中选出3个位置排人，另2个位置排空椅子，有AC种排法，再将4张空椅子中的每两张插入每两人之间，只有1种插法，所以所求的坐法数为A·C=60.

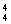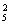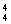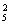(2)可先让4人坐在4个位置上，有A种排法，再让2个“元素”(一个是两个作为一个整体的空位，另一个是单独的空位)插入4个人形成的5个“空当”之间，有A种插法，所以所求的坐法数为A·A=480.

5.用隔板法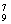：C=C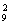=36.　 6. 600;　 7. 18　 6;　 8. 8424.