
4.函数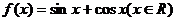 的最小正周期为 .
的最小正周期为 .
3.若抛物线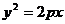 的焦点与椭圆
的焦点与椭圆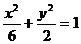 的右焦点重合,则实数
的右焦点重合,则实数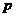 的值是 .
的值是 .
2.等差数列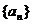 中,公差
中,公差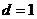 ,
,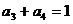 ,则
,则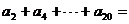 .
.
1.计算: .
.
37、
36、(上海市部分重点中学2008届高三第二次联考)定义在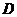 上的函数
上的函数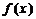 ,如果满足:对任意
,如果满足:对任意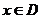 ,存在常数
,存在常数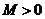 ,都有
,都有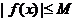 成立,则称
成立,则称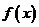 是
是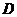 上的有界函数,其中
上的有界函数,其中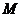 称为函数
称为函数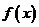 的上界.
的上界.
已知函数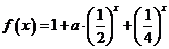 ;
;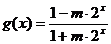 .
.
(1)当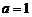 时,求函数
时,求函数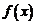 在
在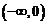 上的值域,并判断函数
上的值域,并判断函数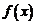 在
在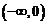 上是否为有界函数,请说明理由;
上是否为有界函数,请说明理由;
(2)若函数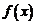 在
在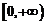 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数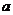 的取值范围;
的取值范围;
(3)若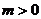 ,函数
,函数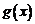 在
在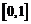 上的上界是
上的上界是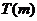 ,求
,求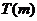 的取值范围.
的取值范围.
[解]:(1)当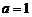 时,
时,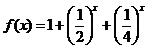
因为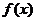 在
在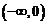 上递减,所以
上递减,所以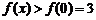 ,即
,即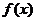 在
在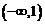 的值域为
的值域为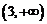
故不存在常数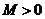 ,使
,使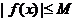 成立
成立
所以函数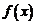 在
在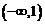 上不是有界函数。 ……4分(没有判断过程,扣2分)
上不是有界函数。 ……4分(没有判断过程,扣2分)
(2)由题意知,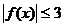 在
在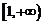 上恒成立。………5分
上恒成立。………5分
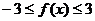 ,
, 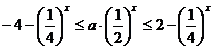
∴ 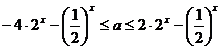 在
在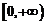 上恒成立………6分
上恒成立………6分
∴ 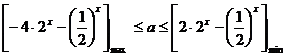 ………7分
………7分
设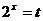 ,
,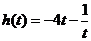 ,
,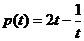 ,由
,由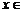
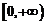 得 t≥1,
得 t≥1,
设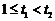 ,
,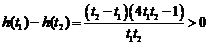
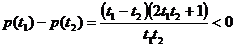
所以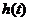 在
在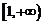 上递减,
上递减,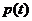 在
在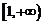 上递增,………9分(单调性不证,不扣分)
上递增,………9分(单调性不证,不扣分)
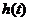 在
在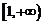 上的最大值为
上的最大值为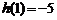 ,
, 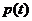 在
在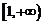 上的最小值为
上的最小值为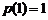
所以实数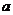 的取值范围为
的取值范围为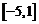 。…………………………………11分
。…………………………………11分
(3)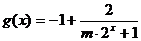 ,
,
∵ m>0 ,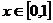 ∴
∴ 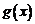 在
在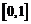 上递减,………12分
上递减,………12分
∴ 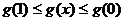 即
即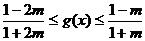 ………13分
………13分
①当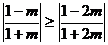 ,即
,即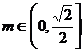 时,
时,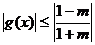 ,
………14分
,
………14分
此时 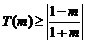 ,………16分
,………16分
②当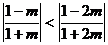 ,即
,即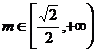 时,
时,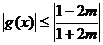 ,
,
此时 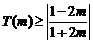 , ---------17分
, ---------17分
综上所述,当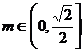 时,
时,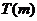 的取值范围是
的取值范围是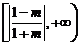 ;
;
当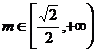 时,
时,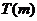 的取值范围是
的取值范围是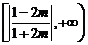 ………18
………18
35、(山东省郓城一中2007-2008学年第一学期期末考试)造船厂年造船量20艘,造船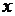 艘产值函数为
艘产值函数为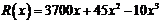 (单位:万元),成本函数
(单位:万元),成本函数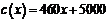 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数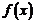 的边际函数
的边际函数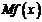 定义为
定义为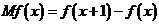
(1)求利润函数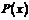 及边际利润函数
及边际利润函数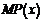 (利润=产值-成本)
(利润=产值-成本)
(2)问年造船量安排多少艘时,公司造船利润最大
(3)边际利润函数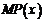 的单调递减区间
的单调递减区间
解:(1)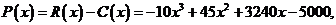
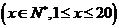 ;
;
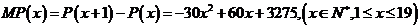
(2)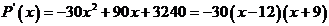
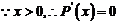 ,
,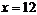
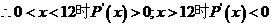 ,
,
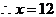 ,
,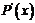 有最大值;即每年建造12艘船,年利润最大(8分)
有最大值;即每年建造12艘船,年利润最大(8分)
(3)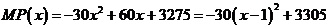 ,(11分)
,(11分)
所以,当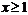 时,
时,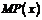 单调递减,所以单调区间是
单调递减,所以单调区间是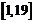 ,且
,且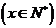
34、(江苏省盐城市2008届高三六校联考)某公司生产一种产品,每年需投入固定成本0.5万元,此外每生产1百件这样的产品,还需增加投入0.25万元,经市场调查知这种产品年需求量为5百件,产品销售数量为t(百件)时,销售所得的收入为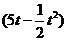 万元
万元
(1)该公司这种产品的年生产量为x百件,生产并销售这种产品所得到的利润为当年产量x的函数f(x),求f(x);
(2)当该公司的年产量为多大时当年所获得的利润最大.
解:(1)当x≤5时,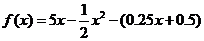
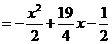 ……5分
……5分
当x>5时 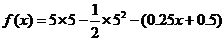 =12-
=12-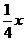 ……………7分
……………7分
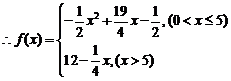 ………………………………………8分
………………………………………8分
(2)当0<x≤5时 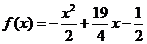 =
=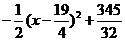
故当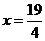 百件=475件时,
百件=475件时,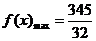 万元 ……………………………12分
万元 ……………………………12分
当x>5时,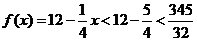
故当该公司的年产量为475件时,当年获得的利润最大。 ……………………14分
33、(江苏省盐城市2008届高三六校联考)已知函数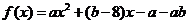 ,当
,当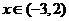 时f(x)>0,
时f(x)>0,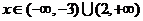 时f(x)<0
时f(x)<0
(1)求y=f(x)的解析式;
(2)c为何值时,不等式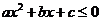 的解集为R.
的解集为R.
解:(1)由x∈(-3,2)时f(x)>0,x∈(-∞,-3)∪(2,+∞)时f(x)>0
知:-3,2是方程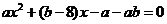 的两根且a<0 …………………3分
的两根且a<0 …………………3分
故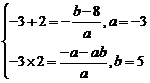 ∴f(x)=-3x2-3x+18 ……………………………7分
∴f(x)=-3x2-3x+18 ……………………………7分
(2)由a<0知二次函数y=ax2+bx+c的图象开口向下
要使-3x2+5x+c≤0的解集为R,只需△≤0 …………………………………10分
25+12c≤0 ∴c≤-
∴当c≤- 时,ax2+bx+c≤0的解集为R …………………………………12分
时,ax2+bx+c≤0的解集为R …………………………………12分
32、(江苏省如东高级中学2008届高三四月份模拟)定义在定义域D内的函数y=f(x),若对任意的x1、x2∈D,都有|f(x1)-f(x2)|<1,则称函数y=f(x)为“Storm函数”.已知函数f(x)=x3-x+a(x∈[-1,1],a∈R).
(1)若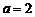 ,求过点
,求过点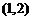 处的切线方程;
处的切线方程;
(2)函数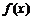 是否为“Storm函数”?如果是,请给出证明;如果不是,请说明理由.
是否为“Storm函数”?如果是,请给出证明;如果不是,请说明理由.
分析:本题属于信息迁移题,主要考查利用导数求函数的极值.
解:(1)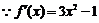 ,
,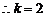 ,
,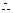 切线方程为
切线方程为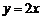 .
.
(2)函数f(x)=x3-x+a(x∈[-1,1],a∈R)的导数是f′(x)=3x2-1,
当3x2-1=0时,即x=±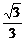 ,
,
当x<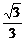 时,f′(x)=3x2-1<0;当x>
时,f′(x)=3x2-1<0;当x>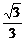 时,f′(x)=3x2-1>0,
时,f′(x)=3x2-1>0,
故f(x)在x∈[-1,1]内的极小值是a-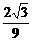 .
.
同理,f(x)在x∈[-1,1]内的极大值是a+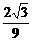 .
.
∵f(1)=f(-1)=a,
∴函数f(x)=x3-x+a(x∈[-1,1],a∈R)的最大值是a+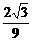 ,最小值是a-
,最小值是a-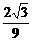 ,
,
因为|f(x1)-f(x2)|<|fmax-fmin|,
故|f(x1)-f(x2)|<|fmax-fmin|=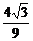 <1.
<1.
所以函数f(x)=x3-x+a(x∈[-1,1],a∈R)是“Storm函数”.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com