
3.(2009年浙江理4)在二项式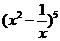 的展开式中,含
的展开式中,含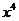 的项的系数是
的项的系数是 学( )
学( )
A.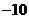 B.
B.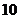
 C.
C.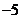 D.
D.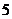

B [解析]对于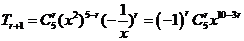 ,对于
,对于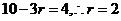 ,则
,则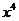 的项的系数是
的项的系数是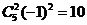
2.(2009年陕西理6)若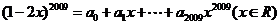 ,则
,则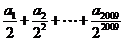 的值为
的值为
(A)2
(B)0
(C)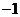 (D)
(D) 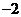


答案:C解析: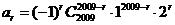 则
则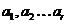 都能表示出来,则
都能表示出来,则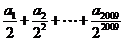 等于
等于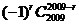 ,再利用倒序相加法求得。
,再利用倒序相加法求得。
1. (2010年陕西理4).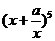 (
(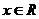 )展开式中
)展开式中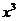 的系数为10,则实数a等于 (D)
的系数为10,则实数a等于 (D)
(A)-1
(B)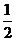 (C) 1
(D) 2
(C) 1
(D) 2
[答案]D[解析]∵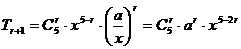 ,又令
,又令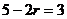 得
得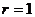 ,∴由题设知
,∴由题设知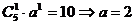 .故选
.故选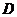 .
.
20. (本小题满分14分)
解: (Ⅰ)由于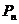 的横坐标构成以
的横坐标构成以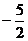 为首项,
为首项,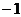 为公差的等差数列
为公差的等差数列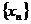 ,
,
故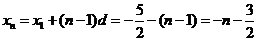 .
……………..3分
.
……………..3分
又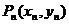 位于函数
位于函数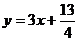 的图象上,
的图象上,
所以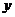
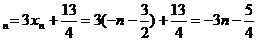 .
………………..5分
.
………………..5分
所求点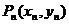 的坐标为(
的坐标为(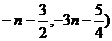 . …………….6分
. …………….6分
(Ⅱ)证明:由题意可设抛物线 的方程为
的方程为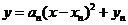 ,即
,即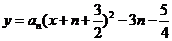 .
.
由抛物线 过点
过点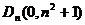 ,于是有
,于是有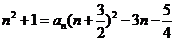 .
.
由此可得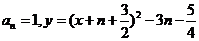 .
………………9分
.
………………9分
故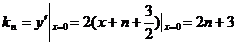 .
.
所以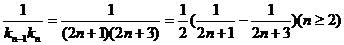 ,
………….11分
,
………….11分
于是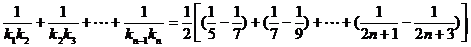
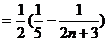 .
.
故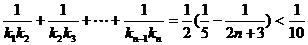 .
………………14分
.
………………14分
19. (本小题满分13分)
解: (Ⅰ) 恰用3发子弹就将油罐引爆记为事件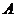 ,则
,则
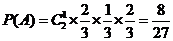 .
.
即恰用3发子弹将油罐引爆的概率为 . ……………………6分
. ……………………6分
(Ⅱ) 记“油罐被引爆”的事件为事件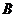 ,其对立事件为
,其对立事件为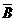 ,则
,则
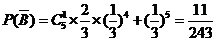 .
……………………10分
.
……………………10分
故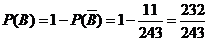 .
.
即油罐被引爆的概率为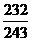 .
…………………13分
.
…………………13分
18.(本小题满分13分)
解:(Ⅰ)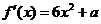 ,
,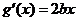 ,
……………..2分
,
……………..2分
根据题意有
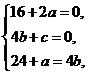 ………………..4分
………………..4分
解得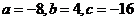 .
……………….6分
.
……………….6分
(Ⅱ)由(Ⅰ)知 =
=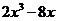 ,
,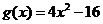 .
.
则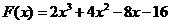 .
…………………. 7分
.
…………………. 7分
 .
………………..8分
.
………………..8分
令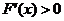 ,即
,即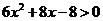 ,解得
,解得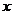 <-2或
<-2或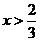 ;
;
令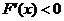 ,即
,即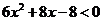 ,解得-2<
,解得-2<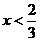 . ………………..11分
. ………………..11分
当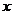 在
在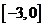 内变化时,
内变化时,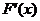 与
与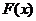 的变化情况如下:
的变化情况如下:
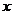 |
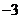 |
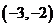 |
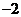 |
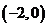 |
0 |
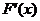 |
+ |
+ |
0 |
- |
- |
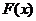 |
-10 |
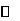 |
极大值 |
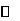 |
-16 |
当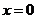 时
时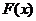 有最小值-16;当
有最小值-16;当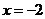 时
时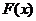 有最大值0.
………………..13分
有最大值0.
………………..13分
17.(本小题满分14分)
解:  (Ⅰ)
(Ⅰ)
证明:连结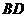 交
交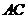 于点
于点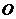 ,连结
,连结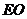 .
.
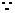
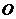 为
为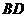 中点,
中点,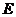 为
为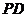 中点,
中点,
∴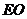 //
//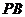 .
…………………3分
.
…………………3分
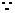
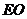
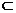 平面
平面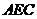 ,
,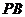
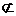 平面
平面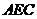 ,
,
∴ 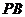 //平面
//平面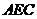 .
…………………6分
.
…………………6分
 (Ⅱ)
(Ⅱ)
解法1:取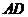 中点
中点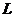 ,过
,过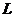 作
作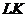
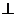
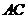 于
于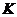 ,连结
,连结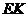 、
、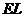 ,
,
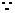
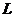 为
为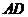 中点,∴
中点,∴ 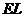 //
//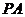 ,∴
,∴
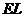
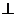 平面
平面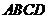 ,
,
∴ 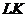 为
为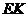 在平面
在平面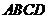 内的射影.
内的射影.
又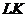
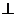
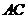 ,
∴
,
∴ 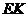
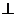
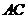 ,
,
∴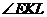 为二面角
为二面角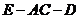 的平面角.
………………10分
的平面角.
………………10分
在Rt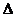
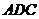 中,
中,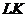
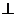
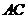 ,
,
∴△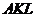 ∽△
∽△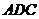 .
.
∴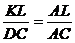 ,设正方形边长为2,
,设正方形边长为2, 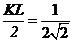 ,∴
,∴
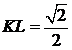 . ………………12分
. ………………12分
在Rt△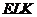 中,
中,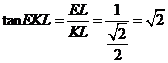 ,
,
∴二面角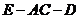 的大小为
的大小为 .
……………14分
.
……………14分
解法2:
 (Ⅱ)如图,以
(Ⅱ)如图,以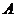 为坐标原点,
为坐标原点,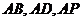 所在直线分别为
所在直线分别为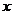 轴,
轴,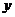 轴,
轴,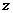 轴建立空间直角坐标系
轴建立空间直角坐标系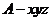 .
………………8分
.
………………8分
由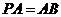 ,设正方形边长为2, 则
,设正方形边长为2, 则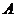 (0,
0, 0),
(0,
0, 0), 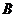 (2,
0, 0),
(2,
0, 0),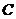 (2,
2, 0),
(2,
2, 0),
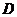 (0,
2, 0),
(0,
2, 0), 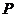 (0,
0, 2),
(0,
0, 2), 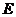 (0,
1, 1) .
……………10分
(0,
1, 1) .
……………10分
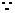
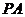
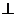 平面
平面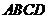 ,∴
,∴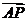 是平面
是平面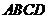 的法向量,
的法向量,
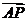 =(0, 0, 2).
=(0, 0, 2).
设平面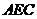 的法向量为
的法向量为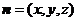 ,
, 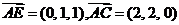 ,
,
则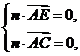 即
即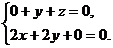 解得
解得 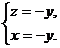
令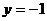 ,则
,则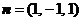 .
………………..12分
.
………………..12分
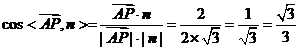 .
.
∴二面角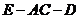 的大小为
的大小为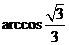 .
………………14分
.
………………14分
16. (本小题满分13分)
解:(Ⅰ)由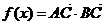 得
得
 =
= 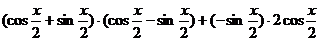 …………..4分
…………..4分
= 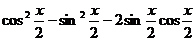
= 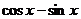 =
=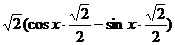
=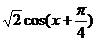 ………………6分
………………6分
所以 的最小正周期
的最小正周期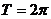 ,
……………8分
,
……………8分
又由
 ,
,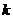 ∈Z,
∈Z,
得
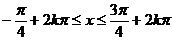 ,
,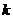 ∈Z.
∈Z.
故 的单调递减区间是
的单调递减区间是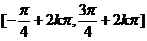 (
(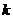 ∈Z).
…………….10分
∈Z).
…………….10分
(Ⅱ)由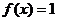 得
得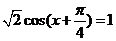 ,故
,故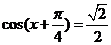 .
.
又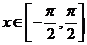 ,于是有
,于是有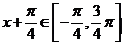 ,得
,得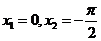 ……………12分
……………12分
所以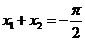 .
……………13分
.
……………13分
15. (本小题满分13分)
解:(Ⅰ)依题意函数 过点(2,-1),有
过点(2,-1),有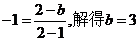 .
.
故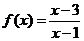 .
………4分
.
………4分
(Ⅱ) 由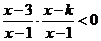 得
得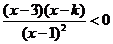 .
.
原不等式等价于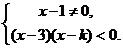 ……………6分
……………6分
当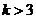 时,
时, 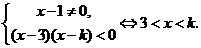 ……………8分
……………8分
当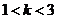 时,
时,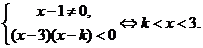 ………………10分
………………10分
当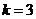 时 ,
时 ,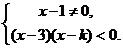 此时不等式组无解
……………12分
此时不等式组无解
……………12分
所以,当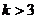 时,不等式的解集为
时,不等式的解集为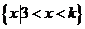 ;当
;当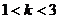 时,不等式的解集为
时,不等式的解集为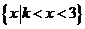 ;
;
当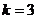 时,不等式的解集为空集.
………………13分
时,不等式的解集为空集.
………………13分
12.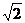 13. 56
14.
13. 56
14.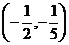
注:两个空的填空题第一个空填对得3分,第二个空填对得2分.lby
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com