
19.(本题满分14分)
设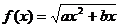 ,求满足下列条件的实数
,求满足下列条件的实数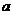 的值:至少有一个正实数
的值:至少有一个正实数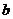 ,使函数
,使函数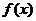 的定义域和值域相同。
的定义域和值域相同。
18.(本题满分14分)
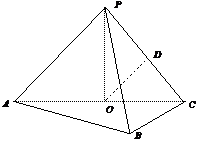 如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC.
(Ⅰ)求证:OD∥平面PAB;
(Ⅱ)当k=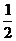 时,求直线PA与平面PBC所成角的正弦值的大小;
时,求直线PA与平面PBC所成角的正弦值的大小;
(Ⅲ) 当k取何值时,O在平面PBC内的射影恰好为△PBC的重心?
16.(本题满分12分)
在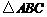 中,
中,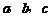 分别是三个内角
分别是三个内角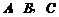 的对边.若
的对边.若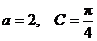 ,
,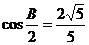 ,求
,求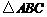 的面积
的面积 .
.
17.(本题满分12分)
有红蓝两粒质地均匀的正方体形状骰子,红色骰子有两个面是8,四个面是2,蓝色骰子有三个面是7,三个面是1,两人各取一只骰子分别随机掷一次,所得点数较大者获胜.
(1)分别求出两只骰子投掷所得点数的分布列及期望;
(2)求投掷蓝色骰子者获胜的概率是多少?
15.(几何证明选讲选做题)如图AB是⊙O的直径, P为AB延长线上一点, PC切⊙O于点C, PC=4,PB=2。则⊙O的半径等于 ;
14.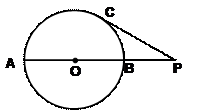 (不等式选讲选做题)函数
(不等式选讲选做题)函数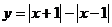 的最大值是
。
的最大值是
。
13.(坐标系与参数方程选做题)设直线参数方程为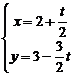 (
(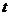 为参数),则它的截距式方程为
。
为参数),则它的截距式方程为
。
12.在如下程序框图中,已知: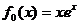 ,则输出的是_________ _.
,则输出的是_________ _.

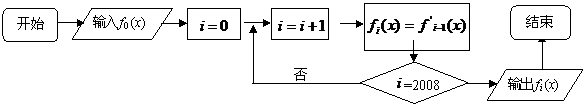
11.已知正实数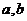 满足等式
满足等式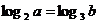 ,给出下列五个等式①
,给出下列五个等式①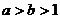 ,②
,②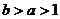 ,③
,③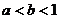 ,④
,④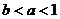 ,⑤
,⑤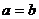 ,其中可能成立的关系式是
(填序号)
,其中可能成立的关系式是
(填序号)
10.在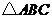 中,
中,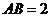 ,
,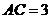 ,
,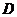 是边
是边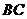 的中点,则
的中点,则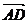 ∙
∙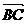 = .
= .
9.某校开设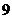 门课程供学生选修,其中
门课程供学生选修,其中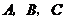 三门由于上课时间相同,至多选一门,学校规定,每位同学选修
三门由于上课时间相同,至多选一门,学校规定,每位同学选修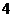 门,共有__ ___种不同的选修方案.(用数值作答)
门,共有__ ___种不同的选修方案.(用数值作答)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com