
5.设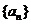 是一个公差为
是一个公差为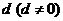 的等差数列,它的前
的等差数列,它的前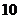 项的和
项的和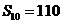 ,且
,且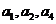
成等比数列.(1)证明: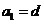 ;(2)求公差
;(2)求公差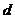 的值和数列
的值和数列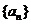 的通项公式.
的通项公式.
4.(1)解:由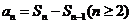 ,得
,得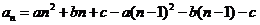 ,
,
即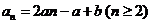 ,而
,而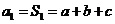 ,
,
当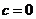 时,
时,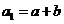 ,满足
,满足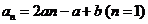 ,
,
即数列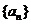 是等差数列;
是等差数列;
当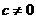 时,
时,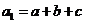 ,不满足
,不满足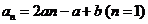 ,
,
即数列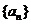 不是等差数列.
不是等差数列.
(2)证明:因为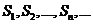 是等比数列,其公比
是等比数列,其公比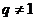 ,
,
所以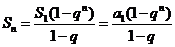 ,
,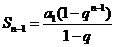 ,
,
而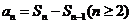 ,
,
得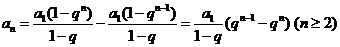 ,
,
而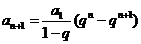 ,则
,则 ,
,
得数列 也是等比数列.
也是等比数列.
4.(1)设数列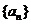 的前
的前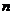 项的和为
项的和为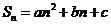 (
(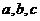 为常数且
为常数且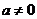 ),试判断
),试判断
数列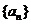 是不是等差数列.
是不是等差数列.
(2)在数列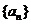 中,其前
中,其前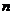 项的和为
项的和为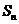 ,且
,且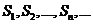 是等比数列,其公比
是等比数列,其公比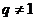 ,
,
求证:数列 也是等比数列.
也是等比数列.
3.解:记前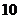 项的和为
项的和为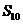 ,前
,前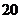 项的和为
项的和为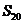 ,前
,前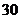 项的和为
项的和为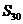 ,
,
则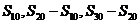 成等比数列,即
成等比数列,即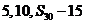 成等比数列,
成等比数列,
得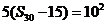 ,即
,即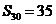 .
.
3.在等比数列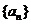 中,已知前
中,已知前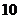 项的和为
项的和为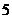 ,前
,前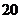 项的和为
项的和为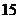 ,求前
,求前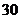 项的和.
项的和.
2.填空题
(1)设等差数列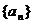 公差为
公差为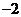 ,如果
,如果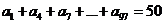 ,
,
那么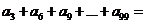 ___________________.
___________________.
(1)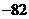
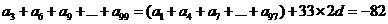 .
.
(2)在等差数列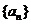 中,若
中,若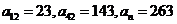 ,则
,则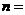 ________________.
________________.
(2)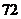
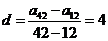 ,
,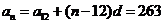 ,
,
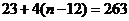 ,得
,得 .
.
(3)在等比数列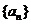 中,若
中,若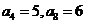 ,则
,则 _______,
_______,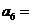 _______.
_______.
(3)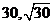
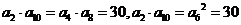 ,而
,而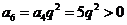 ,得
,得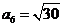 .
.
(4)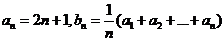 ,则
,则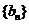 的前
的前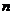 项的和为________________.
项的和为________________.
(4)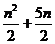
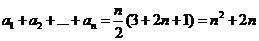 ,得
,得 ,
,
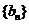 的前
的前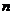 项的和
项的和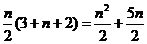 .
.
(5)已知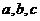 成等差数列,
成等差数列,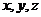 成等比数列,且均为正数,
成等比数列,且均为正数,
则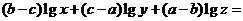 ________________.
________________.
(5)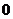 记公差为
记公差为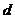 ,
,
则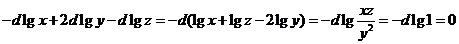 .
.
1.选择题
(1)已知等差数列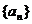 的首项为
的首项为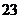 ,公差是整数,从第
,公差是整数,从第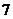 项开始为负值,则公差为( ).
项开始为负值,则公差为( ).
A.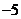 B.
B.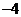 C.
C.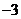 D.
D.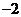
(1)B 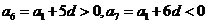 ,即
,即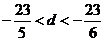 ,得
,得 ,
,
而公差是整数,则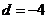 .
.
(2)在等差数列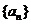 中,
中,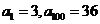 ,则
,则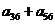 等于( ).
等于( ).
A.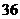 B.
B. C.
C.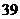 D.
D.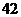
(2)A 由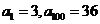 ,得公差
,得公差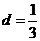 ,
, .
.
(3)数列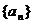 ,
,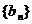 都是等差数列,其中
都是等差数列,其中 ,那么数列
,那么数列
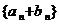 的前
的前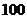 项的和是( ).
项的和是( ).
A.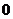 B.
B.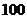 C.
C.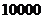 D.
D.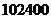
(3)C 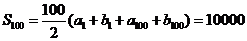 .
.
(4)已知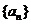 是等比数列,且
是等比数列,且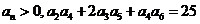 ,那么
,那么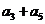 等于( ).
等于( ).
A.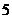 B.
B.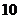 C.
C.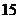 D.
D.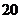
(4)A 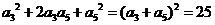 ,而
,而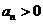 ,则
,则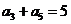 .
.
(5)在等差数列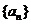 中,若
中,若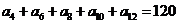 ,则
,则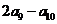 的值( ).
的值( ).
A.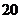 B.
B.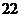 C.
C.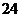 D.
D.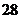
(5)C 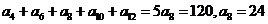 ,
,
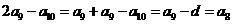 .
.
(6)若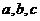 成等比数列,则函数
成等比数列,则函数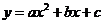 的图象与
的图象与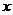 轴交点的个数为( ).
轴交点的个数为( ).
A.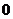 B.
B.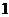 C.
C.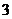 D.不能确定
D.不能确定
(6)A 因为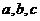 成等比数列,则
成等比数列,则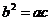 ,得
,得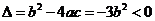 .
.
(7)在等差数列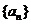 中,若
中,若 ,则
,则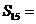 ( ).
( ).
A.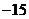 B.
B.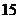 C.
C.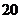 D.
D.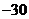
(7)D 由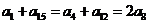 ,得
,得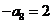 ,即
,即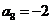 ,
,
而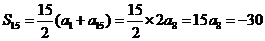 ,得
,得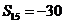 .
.
(8)已知等比数列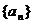 公比
公比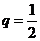 ,且
,且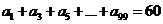 ,则
,则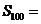 ( ).
( ).
A.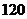 B.
B.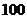 C.
C.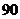 D.
D.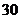
(8)C 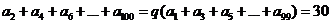 ,
,
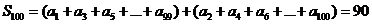 .
.
(9)已知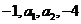 成等差数列,
成等差数列,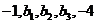 成等比数列,则
成等比数列,则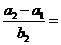 ( ).
( ).
A.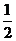 B.
B.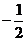 C.
C.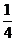 D.
D.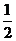 或
或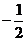
(9)A 由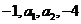 成等差数列,得
成等差数列,得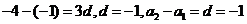 ,
,
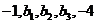 成等比数列,得
成等比数列,得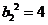 ,而
,而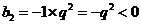 ,即
,即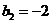 .
.
(10)若某等比数列中前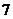 项的和为
项的和为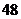 ,前
,前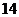 项的和为
项的和为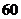 ,则前
,则前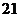 项的和为( ).
项的和为( ).
A.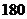 B.
B.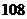 C.
C.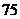 D.
D.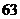
(10)D 记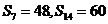 ,则
,则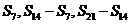 成等比数列,
成等比数列,
即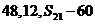 成等比数列,得
成等比数列,得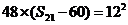 ,得
,得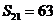 .
.
3.解: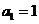 ,
, 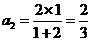 ,
, 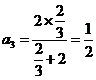 ,
,
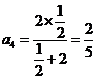 ,
, 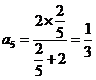 ,
,
观察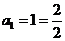 ,
,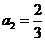 ,
,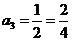 ,
, ,
,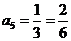 ,
,
归纳得通项公式 .
.
二 等差数列与等比数列 复习题
3.已知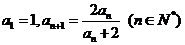 ,写出它的前
,写出它的前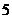 项并归纳出通项公式.
项并归纳出通项公式.
2.解:(1)观察分子是奇数列,分母是成等比数列,
即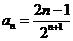 ;
;
(2)观察发现该数列的每一项加上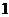 ,就变成完全平方数,
,就变成完全平方数,
即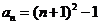 ;
;
(3)观察分子是偶数列,分母是连续奇数的积,
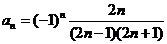 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com