
12.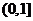 ; 13.
; 13.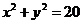
14(Ⅰ)解:AB中点M的坐标是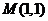 ,
,
中线CM所在直线的方程是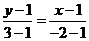 , 即
, 即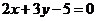
(Ⅱ)解法一: 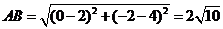 ,………………………………8分
,………………………………8分
直线AB的方程是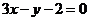 ,
,
点C到直线AB的距离是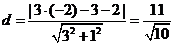 ………………………10分
………………………10分
所以△ABC的面积是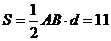 .
…………………………12分
.
…………………………12分
解法二:设AC与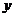 轴的交点为D,则D恰为AC的中点,其坐标是
轴的交点为D,则D恰为AC的中点,其坐标是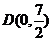 ,
, 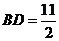 ,
,
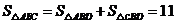 ………………
………………
15;解(Ⅰ)是偶函数. 定义域是R,
∵ 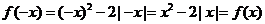 ∴ 函数
∴ 函数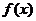 是偶函数.
是偶函数.
(直接证明得正确结论给6分)
(Ⅱ)是单调递增函数. 当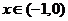 时,
时,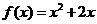
设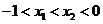 ,则
,则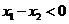 ,且
,且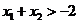 ,即
,即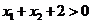
∵ 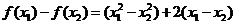
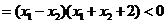
∴ 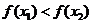 所以函数
所以函数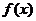 在
在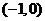 上是单调递增函数.
上是单调递增函数.
7.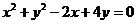 ;8.
;8.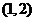 ;9.
;9.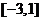 ;10.10 ;11.60°;
;10.10 ;11.60°;
1.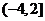 ;2.
;2.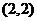 ; 3.
; 3.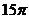 ; 4.2;5.-2;6、向左平移1个单位;
; 4.2;5.-2;6、向左平移1个单位;
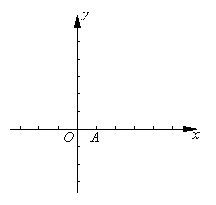
17、已知圆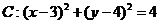 ,直线
,直线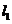 过定点A(1,0).
过定点A(1,0).
(Ⅰ)若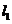 与圆相切,求
与圆相切,求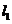 的方程;
的方程;
 (Ⅱ)若
(Ⅱ)若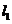 与圆相交于P,Q两点,线段PQ的中点为M,又
与圆相交于P,Q两点,线段PQ的中点为M,又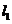 与
与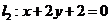 的交点为N,求证:
的交点为N,求证: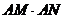 为定值.
为定值.
16、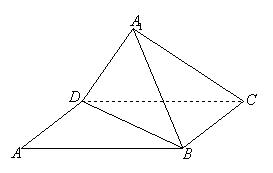 如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到
如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到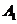 点,且
点,且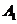 在平面BCD上的射影O恰好在CD上.
在平面BCD上的射影O恰好在CD上.
(Ⅰ)求证: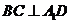 ;
;
(Ⅱ)求证:平面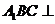 平面
平面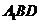 ;
;
(Ⅲ)求三棱锥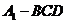 的体积.
的体积.
15、已知函数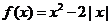 .
.
(Ⅰ)判断并证明函数的奇偶性;
(Ⅱ)判断函数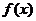 在
在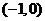 上的单调性并加以证明.
上的单调性并加以证明.
14.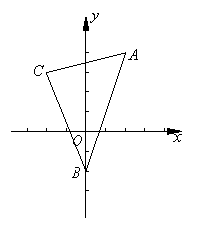 如图,已知三角形的顶点为
如图,已知三角形的顶点为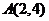 ,
,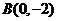 ,
,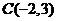 ,
,
求:(Ⅰ)AB边上的中线CM所在直线的方程;
(Ⅱ)求△ABC的面积.
13.以原点为圆心,并与圆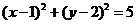 相切的圆的方程是
.
相切的圆的方程是
.
12.函数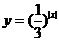 的值域是
.
的值域是
.
11.正四棱锥的底面边长为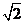 ,体积为
,体积为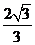 ,则它的侧棱与底面所成的角是
.
,则它的侧棱与底面所成的角是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com