
3.命题“存在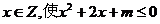 ”的否定是对任意
”的否定是对任意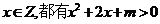 .
.
2.函数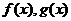 的定义域都为
的定义域都为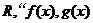 都为奇函数”是“
都为奇函数”是“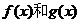 的积为偶函数”的充分非必要条件.
的积为偶函数”的充分非必要条件.
1.关于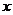 的方程:
的方程: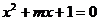 有两个负根的充要条件为
有两个负根的充要条件为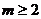 .
.
14.若方程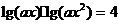 的所有解都大于1,则
的所有解都大于1,则 的取值范围是 .
的取值范围是 .
13.若函数 的图象与
的图象与 轴无公共点,且其图象关于
轴无公共点,且其图象关于 对称,则
对称,则 的值为
.
的值为
.
12.对于在区间 上有意义的两个函数
上有意义的两个函数 ,如果对于任意
,如果对于任意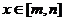 ,均有
,均有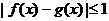 ,则称
,则称 在
在 上是接近的.若函数
上是接近的.若函数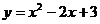 与函数
与函数 在区间
在区间 上是接近的,给出如下区间:①
上是接近的,给出如下区间:①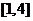 ;②
;② ;③
;③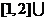
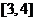 ;④
;④ 则区间
则区间 可以是 .(把你认为正确的序号都填上)
③④
可以是 .(把你认为正确的序号都填上)
③④
11.设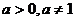 ,函数
,函数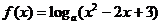 有最小值,则不等式
有最小值,则不等式 的解集为
.
的解集为
.
10.若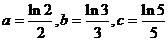 ,则
,则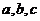 的大小关系为
.
的大小关系为
.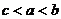
9.已知 是实数,函数
是实数,函数 如果函数
如果函数 在区间
在区间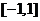 上有零点,则
上有零点,则 的取值范围是
.
的取值范围是
.
8.已知二次函数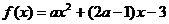 在区间
在区间 上有最大值为1,则实数
上有最大值为1,则实数 的取值集合是
.
的取值集合是
.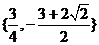
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com