
2、江苏省阜中2008届高三第三次调研考试试题
已知O为坐标原点, 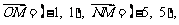 集合
集合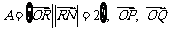
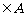 ,且
,且
 .46
.46
3. 已知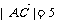 ,
, ,
,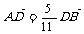 ,
,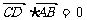 。
。
(1)求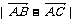 ;
;
(2)设∠BAC=θ,且已知cos(θ+x)=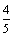 ,
,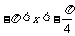 ,求sinx
,求sinx
解:(1)由已知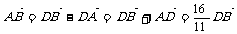
∴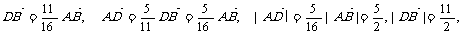
∵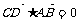 ∴CD⊥AB,在Rt△BCD中BC2=BD2+CD2,
∴CD⊥AB,在Rt△BCD中BC2=BD2+CD2,
又CD2=AC2-AD2, 所以BC2=BD2+AC2-AD2=49, ……4分
所以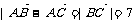 ……6分
……6分
(2)在△ABC中,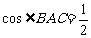 ∴
∴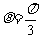 ……8分
……8分

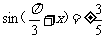
而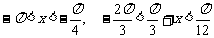 如果
如果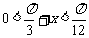 ,
,
则 ∴
∴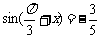 ……10分
……10分
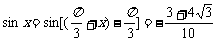
点评:对于平面向量的数量积要学会技巧性应用,解决好实际问题.
题型3:向量的模
例5.(1)已知向量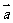 与
与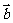 的夹角为
的夹角为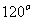 ,
, 则
则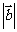 等于( )
等于( )
A.5 B.4 C.3 D.1
(2)(2009辽宁卷文)平面向量a与b的夹角为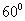 ,a=(2,0), | b |=1,则 | a+2b |等于 ( )
,a=(2,0), | b |=1,则 | a+2b |等于 ( )
A.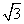 B.2
B.2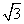 C.4
D.12
C.4
D.12
解析 由已知|a|=2,|a+2b|2=a2+4a·b+4b2=4+4×2×1×cos60°+4=12
∴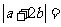
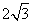
解析:(1)B;(2)B
点评:掌握向量数量积的逆运算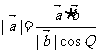 ,以及
,以及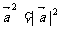 。
。
例6.已知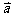 =(3,4),
=(3,4), =(4,3),求x,y的值使(x
=(4,3),求x,y的值使(x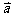 +y
+y )⊥
)⊥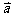 ,且|x
,且|x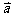 +y
+y |=1。
|=1。
解析:由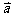 =(3,4),
=(3,4), =(4,3),有x
=(4,3),有x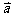 +y
+y =(3x+4y,4x+3y);
=(3x+4y,4x+3y);
又(x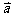 +y
+y )⊥
)⊥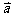
 (x
(x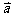 +y
+y )·
)·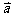 =0
=0 3(3x+4y)+4(4x+3y)=0;
3(3x+4y)+4(4x+3y)=0;
即25x+24y=0 ①;
又|x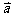 +y
+y |=1
|=1 |x
|x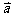 +y
+y |2=1;
|2=1;
 (3x+4y)2+(4x+3y)2=1;
(3x+4y)2+(4x+3y)2=1;
整理得25x2+48xy+25y2=1即x(25x+24y)+24xy+25y2=1 ②;
由①②有24xy+25y2=1 ③;
将①变形代入③可得:y=±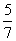 ;
;
再代回①得: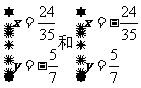 。
。
点评:这里两个条件互相制约,注意体现方程组思想。
题型4:向量垂直、平行的判定
例7.已知向量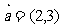 ,
,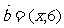 ,且
,且 ,则
,则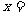 。
。
解析:∵ ,∴
,∴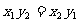 ,∴
,∴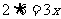 ,∴
,∴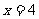 。
。
例8.已知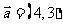 ,
,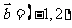 ,
,
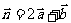 ,按下列条件求实数
,按下列条件求实数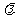 的值。(1)
的值。(1)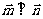 ;(2)
;(2)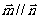 ;
;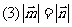 。
。
解析: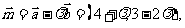
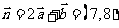
(1)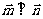
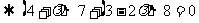
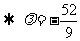 ;
;
(2)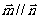
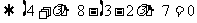
 ;
;
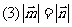
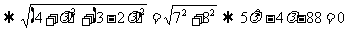
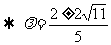 。
。
点评:此例展示了向量在坐标形式下的平行、垂直、模的基本运算.
题型5:平面向量在代数中的应用
例9.已知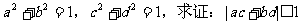 。
。
分析: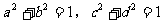 ,可以看作向量
,可以看作向量 的模的平方,而
的模的平方,而 则是
则是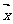 、
、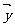 的数量积,从而运用数量积的性质证出该不等式。
的数量积,从而运用数量积的性质证出该不等式。
证明:设
则 。
。
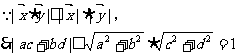
点评:在向量这部分内容的学习过程中,我们接触了不少含不等式结构的式子,如 等。
等。
例10.已知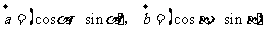 ,其中
,其中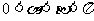 。
。
(1)求证: 与
与 互相垂直;
互相垂直;
(2)若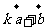 与
与 (
( )的长度相等,求
)的长度相等,求 。
。
解析:(1)因为

所以 与
与 互相垂直。
互相垂直。
(2)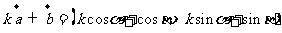 ,
,
 ,
,
所以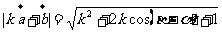 ,
,
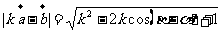 ,
,
因为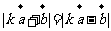 ,
,
所以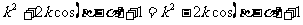 ,
,
有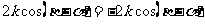 ,
,
因为 ,故
,故 ,
,
又因为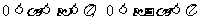 ,
,
所以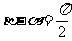 。
。
点评:平面向量与三角函数在“角”之间存在着密切的联系。如果在平面向量与三角函数的交汇处设计考题,其形式多样,解法灵活,极富思维性和挑战性。若根据所给的三角式的结构及向量间的相互关系进行处理。可使解题过程得到简化,从而提高解题的速度。
题型6:平面向量在几何图形中的应用
例12.用向量法证明:直径所对的圆周角是直角。
已知:如图,AB是⊙O的直径,点P是⊙O上任一点(不与A、B重合),求证:∠APB=90°。
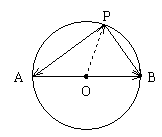
证明:联结OP,设向量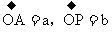 ,则
,则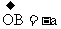 且
且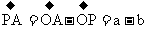 ,
,

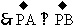 ,即∠APB=90°。
,即∠APB=90°。
点评:平面向量是一个解决数学问题的很好工具,它具有良好的运算和清晰的几何意义。在数学的各个分支和相关学科中有着广泛的应用。
题型7:平面向量在物理中的应用
例13.如图所示,正六边形PABCDE的边长为b,有五个力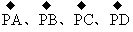 、
、 作用于同一点P,求五个力的合力.
作用于同一点P,求五个力的合力.
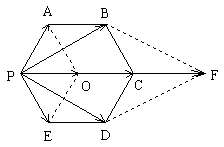
解析:所求五个力的合力为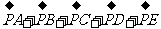 ,如图3所示,以PA、PE为边作平行四边形PAOE,则
,如图3所示,以PA、PE为边作平行四边形PAOE,则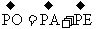 ,由正六边形的性质可知
,由正六边形的性质可知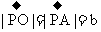 ,且O点在PC上,以PB、PD为边作平行四边形PBFD,则
,且O点在PC上,以PB、PD为边作平行四边形PBFD,则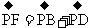 ,由正六边形的性质可知
,由正六边形的性质可知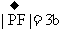 ,且F点在PC的延长线上。
,且F点在PC的延长线上。
由正六边形的性质还可求得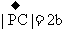
故由向量的加法可知所求五个力的合力的大小为 ,方向与
,方向与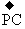 的方向相同。
的方向相同。
课后训练:
(2009北京卷理)已知向量a、b不共线,c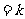 a
a b
b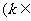 R),d
R),d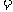 a
a b,如果c
b,如果c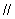 d,那么 ( )
d,那么 ( )
A.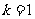 且c与d同向
B.
且c与d同向
B.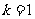 且c与d反向
且c与d反向
C.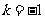 且c与d同向
D.
且c与d同向
D.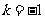 且c与d反向
且c与d反向
答案 D
解析 本题主要考查向量的共线(平行)、向量的加减法. 属于基础知识、基本运算的考
查.
取a ,b
,b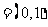 ,若
,若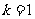 ,则c
,则c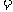 a
a b
b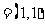 ,d
,d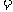 a
a b
b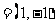 ,
,
显然,a与b不平行,排除A、B.
若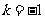 ,则c
,则c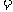
 a
a b
b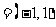 ,d
,d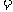
 a
a b
b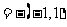 ,
,
即c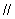 d且c与d反向,排除C,故选D.
d且c与d反向,排除C,故选D.
题型1:数量积的概念
例1.判断下列各命题正确与否:
(1)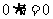 ;
;
(2)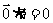 ;
;
(3)若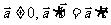 ,则
,则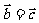 ;
;
(4)若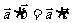 ,则
,则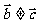 当且仅当
当且仅当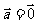 时成立;
时成立;
(5)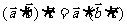 对任意
对任意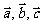 向量都成立;
向量都成立;
(6)对任意向量 ,有
,有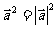 。
。
解析:(1)错;(2)对;(3)错;(4)错;(5)错;(6)对。
点评:通过该题我们清楚了向量的数乘与数量积之间的区别于联系,重点清楚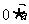 为零向量,而
为零向量,而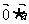 为零.
为零.
例2. 已知△ 中,过重心
中,过重心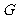 的直线交边
的直线交边 于
于 ,交边
,交边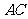 于
于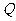 ,设△
,设△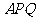 的面积为
的面积为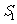 ,△
,△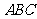 的面积为
的面积为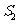 ,
,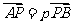 ,
, ,则(ⅰ)
,则(ⅰ) (ⅱ)
(ⅱ)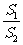 的取值范围是
.
的取值范围是
.
[解析]设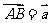 ,
, ,
,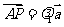 ,
,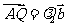 ,因为
,因为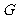 是△
是△ 的重心,故
的重心,故
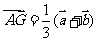 ,又
,又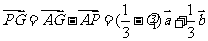 ,
, ,因为
,因为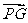 与
与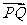 共线,所以
共线,所以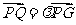 ,即
,即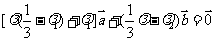 ,又
,又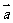 与
与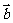 不共线,所以
不共线,所以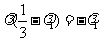 及
及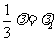 ,消去
,消去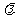 ,得
,得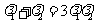 .
.
(ⅰ)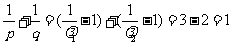 ,故
,故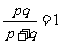 ;
;
(ⅱ)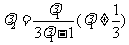 ,那么
,那么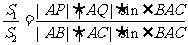

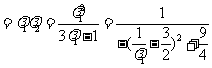 ,当
,当 与
与 重合时,
重合时,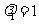 ,当
,当 位于
位于 中点时,
中点时,
 ,故
,故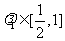 ,故
,故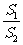
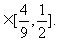 但因为
但因为 与
与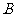 不能重合,故
不能重合,故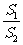
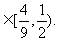

(2)设 、
、 、
、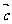 是任意的非零平面向量,且相互不共线,则
是任意的非零平面向量,且相互不共线,则
①( ·
· )
)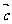 -(
-(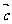 ·
· )
) =
=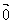 ②|
②| |-|
|-| |<|
|<| -
- | ③(
| ③( ·
·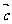 )
) -(
-(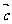 ·
· )
) 不与
不与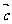 垂直
垂直
④(3 +2
+2 )(3
)(3 -2
-2 )=9|
)=9| |2-4|
|2-4| |2中,是真命题的有( )
|2中,是真命题的有( )
A.①② B.②③ C.③④ D.②④
解析:(1)答案:D;因为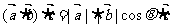 ,而
,而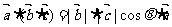 ;而
;而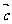 方向与
方向与 方向不一定同向.
方向不一定同向.
(2)答案:D①平面向量的数量积不满足结合律。故①假;②由向量的减法运算可知| |、|
|、| |、|
|、| -
- |恰为一个三角形的三条边长,由“两边之差小于第三边”,故②真;③因为[(
|恰为一个三角形的三条边长,由“两边之差小于第三边”,故②真;③因为[( ·
·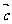 )
) -(
-(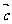 ·
· )
) ]·
]·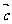 =(
=( ·
·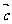 )
) ·
·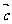 -(
-(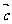 ·
· )
) ·
·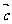 =0,所以垂直.故③假;④(3
=0,所以垂直.故③假;④(3 +2
+2 )(3
)(3 -2
-2 )=9·
)=9· ·
· -4
-4 ·
· =9|
=9| |2-4|
|2-4| |2成立。故④真。
|2成立。故④真。
点评:本题考查平面向量的数量积及运算律,向量的数量积运算不满足结合律。
题型2:向量的夹角
例3.(1)过△ABC的重心任作一直线分别交AB,AC于点D、E.若 ,
,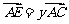 ,
,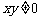 ,则
,则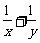 的值为( )
的值为( )
(A)4
(B)3 (C)2
(D)1
解析:取△ABC为正三角形易得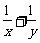 =3.选B.
=3.选B.
评析:本题考查向量的有关知识,如果按常规方法就比较难处理,但是用特殊值的思想就比较容易处理,考查学生灵活处理问题的能力.
(2)已知向量 =(cos
=(cos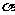 ,sin
,sin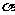 ),
), =(cos
=(cos ,sin
,sin ),且
),且
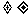
 ,那么
,那么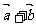 与
与 的夹角的大小是
。
的夹角的大小是
。
(3)已知两单位向量 与
与 的夹角为
的夹角为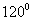 ,若
,若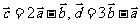 ,试求
,试求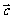 与
与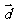 的夹角。
的夹角。
(4)|  |=1,|
|=1,|  |=2,
|=2,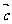 =
=  +
+  ,且
,且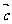 ⊥
⊥ ,则向量
,则向量 与
与 的夹角为 ( )
的夹角为 ( )
A.30° B.60° C.120° D.150°
解析:(2) ;
;
(3)由题意,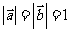 ,且
,且 与
与 的夹角为
的夹角为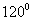 ,
,
所以,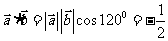 ,
,
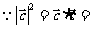
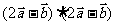
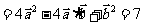 ,
,
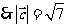 ,
,
同理可得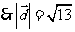 。
。
而
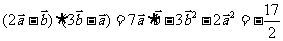 ,
,
设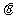 为
为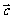 与
与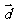 的夹角,
的夹角,
则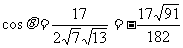 。
。
(4)C;设所求两向量的夹角为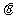


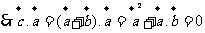

 即:
即: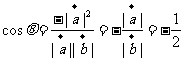

所以

点评:解决向量的夹角问题时要借助于公式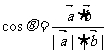 ,要掌握向量坐标形式的运算。向量的模的求法和向量间的乘法计算可见一斑。对于
,要掌握向量坐标形式的运算。向量的模的求法和向量间的乘法计算可见一斑。对于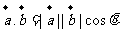 这个公式的变形应用应该做到熟练,另外向量垂直(平行)的充要条件必需掌握.
这个公式的变形应用应该做到熟练,另外向量垂直(平行)的充要条件必需掌握.
例4.(1)设平面向量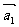 、
、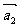 、
、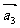 的和
的和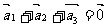 。如果向量
。如果向量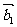 、
、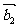 、
、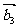 ,满足
,满足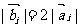 ,且
,且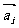 顺时针旋转
顺时针旋转 后与
后与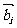 同向,其中
同向,其中 ,则( )
,则( )
A.-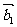 +
+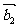 +
+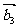 =
=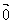 B.
B.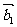 -
-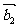 +
+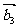 =
=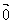

C.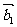 +
+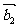 -
-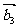 =
=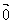 D.
D.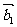 +
+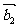 +
+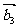 =
=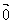
(2)(2009广东卷理)已知向量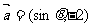 与
与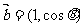 互相垂直,其中
互相垂直,其中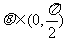 .
.
(1)求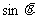 和
和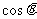 的值;
的值;
(2)若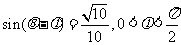 ,求
,求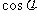 的值.
的值.
解 (1)∵ 与
与 互相垂直,则
互相垂直,则 ,即
,即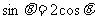 ,代入
,代入 得
得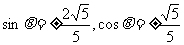 ,又
,又 ,
,
∴ .
.
(2)∵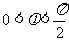 ,
,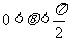 ,∴
,∴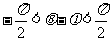 ,
,
则 ,
,
2、(山东临沂2009年模拟)如图,已知△ABC中,|AC|=1,∠ABC=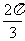 ,∠BAC=θ,记
,∠BAC=θ,记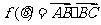 。
。
(1)
求 关于θ的表达式;
关于θ的表达式;
(2)
求 的值域。
的值域。
解:(1)由正弦定理,得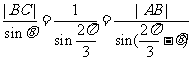
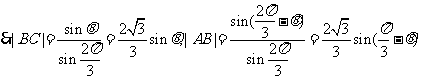
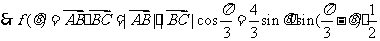
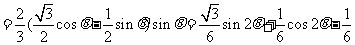
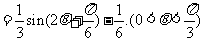
(2)由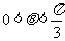 ,得
,得
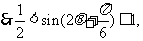
∴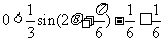 ,即
,即 的值域为
的值域为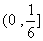 .
.
2.向量的应用
(1)向量在几何中的应用;
(2)向量在物理中的应用。
1.向量的数量积
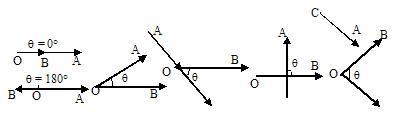
(1)两个非零向量的夹角
已知非零向量a与a,作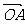 =
= ,
,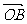 =
= ,则∠AOA=θ(0≤θ≤π)叫
,则∠AOA=θ(0≤θ≤π)叫 与
与 的夹角;
的夹角;
说明:(1)当θ=0时, 与
与 同向;
同向;
(2)当θ=π时, 与
与 反向;
反向;
(3)当θ=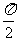 时,
时, 与
与 垂直,记
垂直,记 ⊥
⊥ ;
;
(4)注意在两向量的夹角定义,两向量必须是同起点的,范围0°≤q≤180°。
|

(2)数量积的概念
已知两个非零向量 与
与 ,它们的夹角为
,它们的夹角为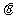 ,则
,则 ·
· =︱
=︱ ︱·︱
︱·︱ ︱cos
︱cos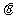 叫做
叫做 与
与 的数量积(或内积)。规定
的数量积(或内积)。规定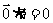 ;
;
向量的投影:︱ ︱cos
︱cos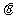 =
=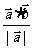 ∈R,称为向量
∈R,称为向量 在
在 方向上的投影。投影的绝对值称为射影;
方向上的投影。投影的绝对值称为射影;
(3)数量积的几何意义:  ·
· 等于
等于 的长度与
的长度与 在
在 方向上的投影的乘积.
方向上的投影的乘积.
(4)向量数量积的性质
①向量的模与平方的关系: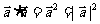 。
。
②乘法公式成立
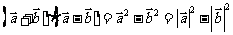 ;
;
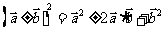
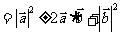 ;
;
③平面向量数量积的运算律
交换律成立: ;
;
对实数的结合律成立: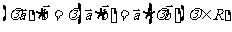 ;
;
分配律成立:
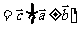 。
。
④向量的夹角:cos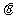 =
=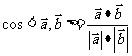 =
=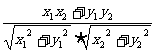 。
。
当且仅当两个非零向量 与
与 同方向时,θ=00,当且仅当
同方向时,θ=00,当且仅当 与
与 反方向时θ=1800,同时
反方向时θ=1800,同时 与其它任何非零向量之间不谈夹角这一问题.
与其它任何非零向量之间不谈夹角这一问题.
(5)两个向量的数量积的坐标运算
已知两个向量 ,则
,则 ·
· =
=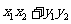 。
。
(6)垂直:如果 与
与 的夹角为900则称
的夹角为900则称 与
与 垂直,记作
垂直,记作 ⊥
⊥ 。
。
两个非零向量垂直的充要条件: ⊥
⊥
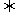
 ·
· =O
=O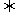
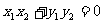 ,平面向量数量积的性质。
,平面向量数量积的性质。
(7)平面内两点间的距离公式
设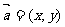 ,则
,则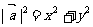 或
或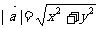 。
。
如果表示向量 的有向线段的起点和终点的坐标分别为
的有向线段的起点和终点的坐标分别为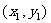 、
、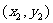 ,那么
,那么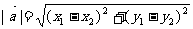 (平面内两点间的距离公式) .
(平面内两点间的距离公式) .
本讲以选择题、填空题考察本章的基本概念和性质,重点考察平面向量的数量积的概念及应用。重点体会向量为代数几何的结合体,此类题难度不大,分值5~9分。
平面向量的综合问题是“新热点”题型,其形式为与直线、圆锥曲线、三角函数等联系,解决角度、垂直、共线等问题,以解答题为主.
预测2010年高考:
(1)一道选择题和填空题,重点考察平行、垂直关系的判定或夹角、长度问题;属于中档题目.
(2)一道解答题,可能以三角、数列、解析几何为载体,考察向量的运算和性质;
2.向量的应用
经历用向量方法解决某些简单的平面几何问题、力学问题与其他一些实际问题的过程,体会向量是一种处理几何问题、物理问题等的工具,发展运算能力和解决实际问题的能力。
1.平面向量的数量积
①通过物理中"功"等实例,理解平面向量数量积的含义及其物理意义;
②体会平面向量的数量积与向量投影的关系;
③掌握数量积的坐标表达式,会进行平面向量数量积的运算;
④能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系。
在复习过程中抓住以下几点:
(1)坚持源于课本、高于课本,以考纲为纲的原则。高考命题的依据是《高考说明》.并明确考点及对知识点与能力的要求作出了明确规定,其实质是精通课本,而本章考题大多数是课本的变式题,即源于课本,因此掌握双基、精通课本是关键;
(2)在注重解题方法、数学思想的应用的同时注意一些解题技巧,椭圆、双曲线、抛物线的定义揭示了各自存在的条件、性质及几何特征与圆锥曲线的焦点、焦半径、准线、离心率有关量的关系问题,若能用定义法,可避免繁琐的推理与运算;
(3)焦半径公式:抛物线上一点P(x1,y1),F为抛物线的焦点,对于四种抛物线的焦半径公式分别为(p>0):
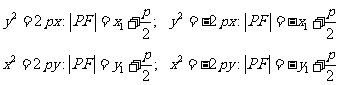
题型1:椭圆的概念及标准方程
例1.求适合下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别是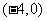 、
、 ,椭圆上一点
,椭圆上一点 到两焦点距离的和等于
到两焦点距离的和等于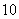 ;
;
(2)两个焦点的坐标分别是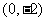 、
、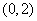 ,并且椭圆经过点
,并且椭圆经过点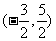 ;
;
(3)焦点在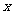 轴上,
轴上,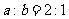 ,
,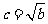 ;
;
(4)焦点在 轴上,
轴上,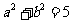 ,且过点
,且过点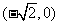 ;
;
(5)焦距为 ,
,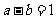 ;
;
(6)椭圆经过两点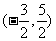 ,
,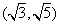 。
。
解析:(1)∵椭圆的焦点在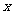 轴上,故设椭圆的标准方程为
轴上,故设椭圆的标准方程为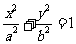 (
(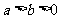 ),
),
∵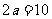 ,
,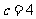 ,∴
,∴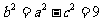 ,
,
所以,椭圆的标准方程为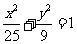 。
。
(2)∵椭圆焦点在 轴上,故设椭圆的标准方程为
轴上,故设椭圆的标准方程为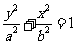 (
(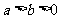 ),
),
由椭圆的定义知,
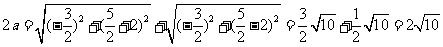 ,
,
∴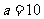 ,又∵
,又∵ ,∴
,∴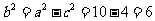 ,
,
所以,椭圆的标准方程为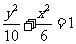 。
。
(3)∵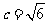 ,∴
,∴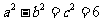 ,①
,①
又由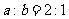 代入①得
代入①得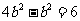 ,
,
∴ ,∴
,∴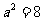 ,又∵焦点在
,又∵焦点在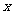 轴上,
轴上,
所以,椭圆的标准方程为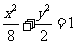 。
。
(4)设椭圆方程为 ,
,
∴ ,∴
,∴ ,
,
又∵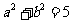 ,∴
,∴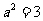 ,
,
所以,椭圆的标准方程为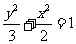 .
.
(5)∵焦距为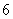 ,∴
,∴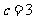 ,
,
∴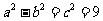 ,又∵
,又∵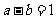 ,∴
,∴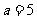 ,
,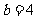 ,
,
所以,椭圆的标准方程为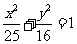 或
或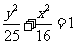 .
.
(6)设椭圆方程为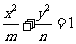 (
(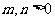 ),
),
由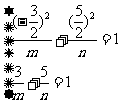 得
得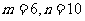 ,
,
所以,椭圆方程为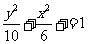 .
.
点评:求椭圆的方程首先清楚椭圆的定义,还要知道椭圆中一些几何要素与椭圆方程间的关系.
例2.(1)(06山东)已知椭圆中心在原点,一个焦点为F(-2 ,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 。
,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 。
(2)(06天津理,8)椭圆的中心为点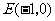 ,它的一个焦点为
,它的一个焦点为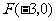 ,相应于焦点
,相应于焦点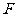 的准线方程为
的准线方程为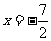 ,则这个椭圆的方程是( )
,则这个椭圆的方程是( )
A.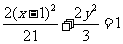 B.
B.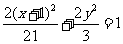

C. D.
D.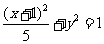

解析:(1)已知 为所求;
为所求;
(2)椭圆的中心为点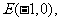 它的一个焦点为
它的一个焦点为

∴ 半焦距 ,相应于焦点F的准线方程为
,相应于焦点F的准线方程为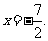

∴ 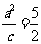 ,
,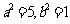 ,则这个椭圆的方程是
,则这个椭圆的方程是 ,选D。
,选D。
点评:求椭圆方程的题目属于中低档题目,掌握好基础知识就可以。
题型2:椭圆的性质
例3.(1)(06山东理,7)在给定椭圆中,过焦点且垂直于长轴的弦长为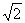 ,焦点到相应准线的距离为1,则该椭圆的离心率为( )
,焦点到相应准线的距离为1,则该椭圆的离心率为( )
(A)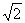 (B)
(B)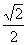 (C)
(C) 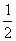 (D)
(D)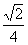
(2)(2009全国卷Ⅰ理)设双曲线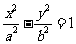 (a>0,b>0)的渐近线与抛物线y=x2
+1相切,则该双曲线的离心率等于( )
(a>0,b>0)的渐近线与抛物线y=x2
+1相切,则该双曲线的离心率等于( )
A.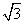 B.2
C.
B.2
C.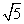 D.
D.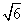
[解析]设切点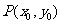 ,则切线的斜率为
,则切线的斜率为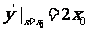 .
.
由题意有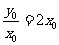 又
又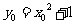
解得: 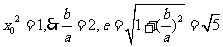 .
.
[答案]C
点评:本题重点考查了椭圆和双曲线的基本性质。
例4.(1)((2009全国卷Ⅰ理)已知椭圆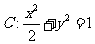 的右焦点为
的右焦点为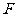 ,右准线为
,右准线为 ,点
,点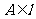 ,线段
,线段 交
交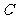 于点
于点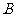 ,若
,若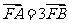 ,则
,则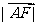 =( )
=( )
A. 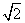 B.
2 C.
B.
2 C.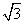 D. 3
D. 3
[解析]过点B作 于M,并设右准线
于M,并设右准线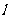 与x轴的交点为N,易知FN=1.由题意
与x轴的交点为N,易知FN=1.由题意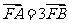 ,故
,故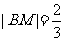 .又由椭圆的第二定义,得
.又由椭圆的第二定义,得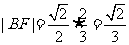
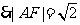 .故选A
.故选A
[答案]A
(2)(2009浙江理)过双曲线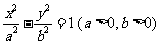 的右顶点
的右顶点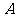 作斜率为
作斜率为 的直线,该直线与双曲线的两条渐近线的交点分别为
的直线,该直线与双曲线的两条渐近线的交点分别为 .若
.若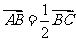 ,则双曲线的离心率是 ( )
,则双曲线的离心率是 ( )
A.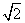 B.
B.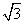 C.
C.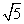 D.
D.
[解析]对于 ,则直线方程为
,则直线方程为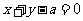 ,直线与两渐近线的交点为B,C,
,直线与两渐近线的交点为B,C,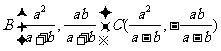 则有
则有
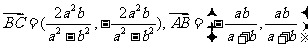 ,因
,因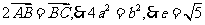 .
.
[答案]C
题型3:双曲线的方程
例5.(1)已知焦点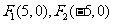 ,双曲线上的一点
,双曲线上的一点 到
到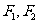 的距离差的绝对值等于
的距离差的绝对值等于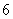 ,求双曲线的标准方程;
,求双曲线的标准方程;
(2)求与椭圆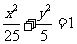 共焦点且过点
共焦点且过点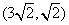 的双曲线的方程;
的双曲线的方程;
(3)已知双曲线的焦点在 轴上,并且双曲线上两点
轴上,并且双曲线上两点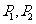 坐标分别为
坐标分别为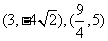 ,求双曲线的标准方程。
,求双曲线的标准方程。
解析:(1)因为双曲线的焦点在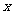 轴上,所以设它的标准方程为
轴上,所以设它的标准方程为
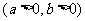 ,
,
∵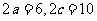 ,∴
,∴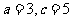 ,∴
,∴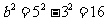 。
。
所以所求双曲线的方程为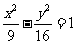 ;
;
(2)椭圆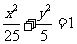 的焦点为
的焦点为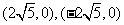 ,可以设双曲线的方程为
,可以设双曲线的方程为 ,则
,则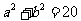 。
。
又∵过点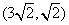 ,∴
,∴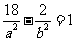 。
。
综上得,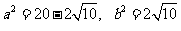 ,所以
,所以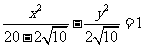 。
。
点评:双曲线的定义;方程确定焦点的方法;基本量 之间的关系。
之间的关系。
(3)因为双曲线的焦点在 轴上,所以设所求双曲线的标准方程为
轴上,所以设所求双曲线的标准方程为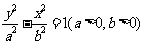 ①;
①;
∵点 在双曲线上,∴点
在双曲线上,∴点 的坐标适合方程①。
的坐标适合方程①。
将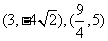 分别代入方程①中,得方程组:
分别代入方程①中,得方程组: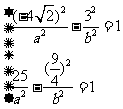
将 和
和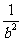 看着整体,解得
看着整体,解得 ,
,
∴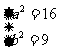 即双曲线的标准方程为
即双曲线的标准方程为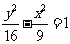 。
。
点评:本题只要解得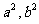 即可得到双曲线的方程,没有必要求出
即可得到双曲线的方程,没有必要求出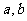 的值;在求解的过程中也可以用换元思想,可能会看的更清楚.
的值;在求解的过程中也可以用换元思想,可能会看的更清楚.
例6.已知双曲线中心在原点,一个顶点的坐标为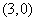 ,且焦距与虚轴长之比为
,且焦距与虚轴长之比为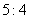 ,则双曲线的标准方程是____________________.
,则双曲线的标准方程是____________________.
解析:双曲线中心在原点,一个顶点的坐标为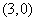 ,则焦点在x轴上,且a=3,焦距与虚轴长之比为
,则焦点在x轴上,且a=3,焦距与虚轴长之比为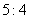 ,即
,即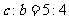 ,解得
,解得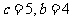 ,则双曲线的标准方程是
,则双曲线的标准方程是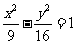 ;
;
点评:本题主要考查双曲线的基础知识以及综合运用知识解决问题的能力。充分挖掘双曲线几何性质,数形结合,更为直观简捷.
题型4:双曲线的性质
例7.(1)(2009安徽卷理)下列曲线中离心率为 的是
的是
A. B.
B.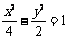 C.
C.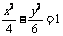 D.
D.
[解析]由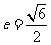 得
得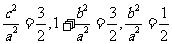 ,选B.
,选B.
[答案]B
(2)(2009江西卷文)设 和
和 为双曲线
为双曲线 (
(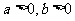 )的两个焦点, 若
)的两个焦点, 若 ,
,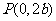 是正三角形的三个顶点,则双曲线的离心率为
是正三角形的三个顶点,则双曲线的离心率为
A.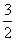 B.
B.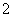 C.
C.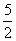 D.3
D.3
[解析]由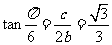 有
有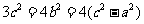 ,则
,则 ,故选B.
,故选B.
[答案]B
(3)(2009天津卷文)设双曲线 的虚轴长为2,焦距为
的虚轴长为2,焦距为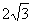 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A.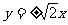 B .
B .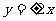 C .
C .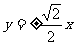 D.
D.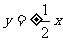
[解析]由已知得到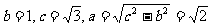 ,因为双曲线的焦点在x轴上,故渐近线方程为
,因为双曲线的焦点在x轴上,故渐近线方程为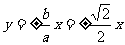
[答案]C
[考点定位]本试题主要考查了双曲线的几何性质和运用。考察了同学们的运算能力和推理能力。
例8.(1)(2009湖北卷理)已知双曲线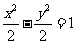 的准线过椭圆
的准线过椭圆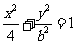 的焦点,则直线
的焦点,则直线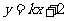 与椭圆至多有一个交点的充要条件是( )
与椭圆至多有一个交点的充要条件是( )
A. 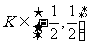 B.
B. 
C. 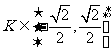 D.
D. 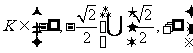
[解析]易得准线方程是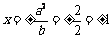
所以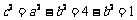 即
即 所以方程是
所以方程是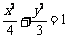
联立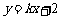 可得
可得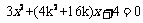 由
由 可解得A.
可解得A.
[答案]A
(2)(2009四川卷文、理)已知双曲线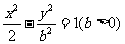 的左、右焦点分别是
的左、右焦点分别是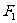 、
、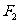 ,其一条渐近线方程为
,其一条渐近线方程为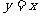 ,点
,点 在双曲线上.则
在双曲线上.则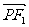 ·
·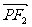 =( )
=( )
A. -12 B. -2 C. 0 D. 4
[解析]由渐近线方程为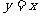 知双曲线是等轴双曲线,∴双曲线方程是
知双曲线是等轴双曲线,∴双曲线方程是 ,于是两焦点坐标分别是(-2,0)和(2,0),且
,于是两焦点坐标分别是(-2,0)和(2,0),且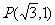 或
或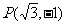 .不妨去
.不妨去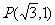 ,则
,则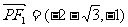 ,
,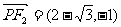 .
.
∴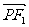 ·
·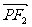 =
=
[答案]C
(3)(2009全国卷Ⅱ理)已知双曲线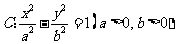 的右焦点为
的右焦点为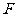 ,过
,过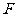 且斜率为
且斜率为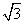 的直线交
的直线交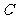 于
于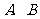 两点,若
两点,若 ,则
,则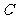 的离心率为
( )
的离心率为
( )
A.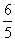 B.
B. 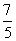 C.
C.
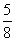 D.
D.
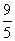
[解析]设双曲线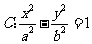 的右准线为
的右准线为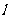 ,过
,过 分 别作
分 别作 于
于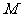 ,
,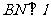 于
于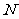 ,
, 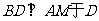 ,由直线AB的斜率为
,由直线AB的斜率为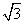 ,知直线AB的倾斜角
,知直线AB的倾斜角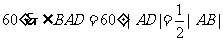 ,
,
由双曲线的第二定义有
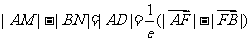
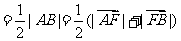 .
.
又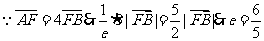 .
.
[答案]A
题型5:抛物线方程
例9.(1))焦点到准线的距离是2;
(2)已知抛物线的焦点坐标是F(0,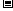 2),求它的标准方程.
2),求它的标准方程.
解析:(1)y =4x,y
=4x,y =
=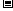 4x,x
4x,x =4y,x
=4y,x =
=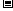 4y;
4y;
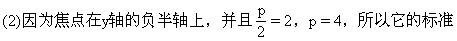
方程是x =
=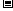 8y。
8y。
点评:由于抛物线的标准方程有四种形式,且每一种形式中都只含一个系数p,因此只要给出确定p的一个条件,就可以求出抛物线的标准方程。当抛物线的焦点坐标或准线方程给定以后,它的标准方程就唯一确定了;若抛物线的焦点坐标或准线方程没有给定,则所求的标准方程就会有多解。
题型6:抛物线的性质
例10.(1)若抛物线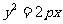 的焦点与椭圆
的焦点与椭圆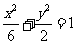 的右焦点重合,则
的右焦点重合,则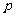 的值为( )
的值为( )
A. B.
B.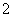 C.
C. D.
D.
(2)抛物线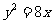 的准线方程是( )
的准线方程是( )
(A) 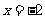 (B)
(B) 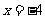 (C)
(C)  (D)
(D)
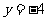
(3)(2009湖南卷文)抛物线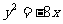 的焦点坐标是(
)
的焦点坐标是(
)
A.(2,0) B.(- 2,0) C.(4,0) D.(- 4,0)
解析:(1)椭圆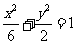 的右焦点为(2,0),所以抛物线
的右焦点为(2,0),所以抛物线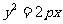 的焦点为(2,0),则
的焦点为(2,0),则 ,故选D;
,故选D;
(2)2p=8,p=4,故准线方程为x=-2,选A;
(3)[解析]由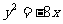 ,易知焦点坐标是
,易知焦点坐标是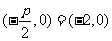 ,故选B.
,故选B.
[答案]B
点评:考察抛物线几何要素如焦点坐标、准线方程的题目根据定义直接计算机即可。
例11.(1)(全国卷I)抛物线 上的点到直线
上的点到直线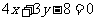 距离的最小值是( )
距离的最小值是( )
A.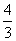 B.
B.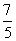 C.
C.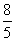 D.
D.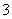
(2)对于顶点在原点的抛物线,给出下列条件:
①焦点在y轴上;
②焦点在x轴上;
③抛物线上横坐标为1的点到焦点的距离等于6;
④抛物线的通径的长为5;
⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1)。
(3)对于抛物线y2=4x上任意一点Q,点P(a,0)都满足|PQ|≥|a|,则a的取值范围是( )
A.(-∞,0) B.(-∞,2 C.[0,2] D.(0,2)
C.[0,2] D.(0,2)
能使这抛物线方程为y2=10x的条件是 .(要求填写合适条件的序号)
解析:(1)设抛物线 上一点为(m,-m2),该点到直线
上一点为(m,-m2),该点到直线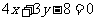 的距离为
的距离为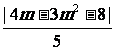 ,当m=
,当m=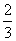 时,取得最小值为
时,取得最小值为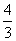 ,选A;
,选A;
(2)答案:②,⑤
解析:从抛物线方程易得②,分别按条件③、④、⑤计算求抛物线方程,从而确定⑤。
(3)答案:B
解析:设点Q的坐标为( ,y0),
,y0),
由 |PQ|≥|a|,得y02+( -a)2≥a2.
-a)2≥a2.
整理,得:y02(y02+16-8a)≥0,
∵y02≥0,∴y02+16-8a≥0.
即a≤2+ 恒成立.而2+
恒成立.而2+ 的最小值为2.
的最小值为2.
∴a≤2.选B。
点评:抛物线问题多考察一些距离、最值及范围问题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com