
2.知道化肥、农药对人体健康的危害,增强环保意识。树立合理使用化肥、农药的观点。
教学重点、难点:化肥、农药对农作物的影响及对人体的危害
教学过程
[创设情景引入]在农村地区,为了促进农作物的生长,常使用化肥与农药。请大家通过回忆列举几种常见的化肥与农药,并说明它们的作用。
[板书]§1.4.3 化肥、农药的安全使用
[总结]常见的化肥有氮肥、磷肥、钾肥、复合肥等,使用化肥的主要目的是提供作物生长所属要的营养元素。常见的农药有敌敌畏、乐果、甲胺磷等,使用农药的主要目的是杀死影响植物生长的害虫和杂草等。
[展示]
|
类型 |
主要物质 |
|
氮肥 |
NH4HCO3 、NH4Cl 、 (NH4)2SO4 、 NH4NO3 |
|
尿素 [CO(NH2)2] |
|
|
磷肥 |
过磷酸钙 [Ca(H2PO4)2 和 CaSO4]
|
|
重过磷酸钙 [Ca(H2PO4)2] |
|
 钾肥 钾肥 |
草木灰 [K2CO3] |
|
KCl |
[提问]化肥板结,不但可能降低肥效,还有可能引发安全事故。请大家讨论第33页“各抒己见”,对合理使用已板结的硝酸铵提出建议。
[讨论、总结]对于已板结的硝酸铵,绝对不能采用敲击的方法加以粉碎,可以将其溶于水后使用。
[讲解]为了更好地促进作物的生长,有时需要将化肥混合使用,但需要注意的是,将化肥混用有时可能导致肥效下降。例如,由于铵态氮肥显酸性,草木灰显碱性,将两者混合使用时会发生反应,导致铵态氮肥肥效下降。为了解决这个问题,人们常使用含氮、磷、钾元素的复合肥。
[提问]目前使用的农药大都具有一定的毒性,因此在储存和使用农药时更应注意安全。请大家讨论有关农药使用时的几个问题:
为什么盛放农药的容器不能随处清洗?不能用来盛放食品?
在食用瓜、果、蔬菜时应注意什么问题?[讨论、小结]在使用化肥、农药时,应防止农药与皮肤接触,更应防止农药通过各种途径进入消化道。因此,盛放农药的容器不能随处清洗,洗涤液不能流入饮用水源,更不能用这样的容器来盛放食品。在食用瓜、果、蔬菜前应将其浸泡几分钟以除去残留的农药,绝对不能食用刚喷洒过农药的瓜、果、蔬菜。
[提问]若不慎发生农药中毒事故,应立即清除毒物并送医院治疗。请大家完成第35页“交流与讨论”,解释所采用的解毒方法的原理。
[讨论、小结]由于敌敌畏、甲胺磷等均为磷酸酯,性质和有机酸酯类似,在碱性条件下水解比较完全,但若用强碱会引起腐蚀,因此常用NaHCO3溶液洗肠。使用泻药的目的是尽快排出体内的毒物。
[小资料]化肥、农药过量使用问题严重
近年来,在耕地面积不断减少的情况下,化肥的使用量一直处于上升态势。2004年全国化肥使用总量已达到4637万吨,比上一年增长5.1%。我国耕地面积不到世界的1/10,但是,氮肥使用量为世界的30%,每公顷高出世界平均水平2.05倍;磷肥的使用量为世界的26%,每公顷高出世界平均水平1.86倍。使用化肥的强度平均每公顷达400公斤(太湖流域曾高达600公斤),平均使用量是发达国家化肥安全使用上限的2倍,远远超过发达国家为防止水体污染而设置的225公斤/公顷的安全标准。
由于氮肥过量使用,未被植物吸收的部分,通过地表径流、淋洗和蒸发等导致了一系列环境问题。中国科学院南京土壤研究所的研究显示,每年我国有123.5万吨氮通过地表水径流到江河湖泊,49.4万吨进入地下水,299万吨进入大气。长江、黄河和珠江每年输出的溶解态无机氮达到97.5万吨,其中90%来自农业,而氮肥占了50%。
我国不仅是世界上最大的化肥使用国,也是最大的农药使用国。1983年农药的使用量是86.2万吨,而到了2003年,仅仅十年时间,全国农药使用量就达到132.5万吨。在一些高产地区,每年施用农药30多次,每公顷用量高达300公斤,有的甚至超过450公斤,过量使用、利用率低的问题十分严重。
[小资料]农业污染危害严重
1.了解化肥、农药对农作物生长的影响,知道合理施加的必要性;
1.了解农业生产中常见化肥的主要成分及对植物生长的作用,认识合理使用化肥的必要性。2.了解常见农药的组成、对环境的影响以及对人体健康的危害,知道常见的防止农药中毒的措施。
过程与方法:通过走访等方式了解化肥、农药对农作物生长的影响。
情感态度与价值观
21.(本小题12分)已知{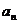 }是正数组成的数列,
}是正数组成的数列,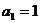 ,且点
,且点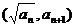
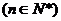 在函数
在函数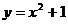 的图象上.
的图象上.
(1)求数列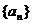 的通项公式;
的通项公式;
(2)若数列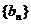 满足
满足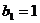 ,
,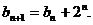 求证:
求证: 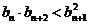 .
.
20.(本小题12分)设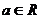 .
. 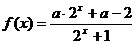
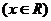
(1)确定a的值,使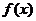 为奇函数;
为奇函数;
(2)当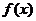 为奇函数时,对于给定的正数
为奇函数时,对于给定的正数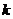 , 解不等式
, 解不等式 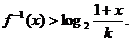
19.(本小题12分)已知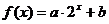 的图象经过点A(1,
的图象经过点A(1,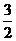 ),B(2,
),B(2,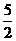 )
)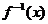 是函数
是函数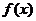 的反函数.
的反函数.
(1)求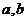 的值;
的值;
(2)若函数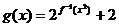 ,求
,求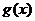 的单调增区间.
的单调增区间.
18.(本小题13分)已知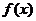 =
=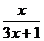 ,数列{
,数列{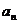 }满足
}满足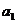 =1,
=1,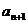 =
=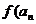 ),(
),(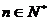 )
)
(1)求证数列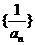 是等差数列;
是等差数列;
(2)求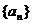 的通项公式.
的通项公式.
17.(本小题13分)已知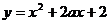
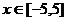
(1)当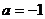 时,求函数
时,求函数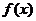 的最大值与最小值;
的最大值与最小值;
(2)求实数a的取值范围,使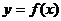 在
在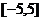 上是单调函数.
上是单调函数.
16.(本小题13分)已知A={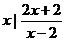
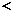 1},B={
1},B={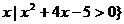 ,
,
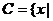
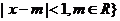 .
.
(1)求A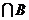 ;
;
(2)若(A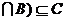 ,求
,求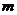 的取值范围.
的取值范围.
15.对于给定的函数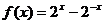 ,有以下四个结论:
,有以下四个结论:
①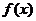 的图象关于原点对称; ②
的图象关于原点对称; ②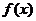 在R上是增函数;
在R上是增函数;
③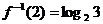 ; ④
; ④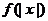 的最小值是0.
的最小值是0.
其中正确命题的序号是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com