
7.定义在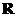 上的函数
上的函数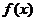 满足
满足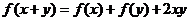 (
(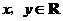 ),
),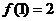 ,则
,则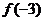 等于_______________.
等于_______________.
6.已知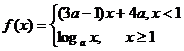 是
是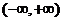 上的减函数,那么
上的减函数,那么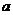 的取值范围是_______.
的取值范围是_______.
5.若不等式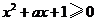 对一切
对一切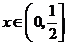 成立,则
成立,则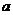 的最小值为_______________.
的最小值为_______________.
4.设函数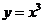 与
与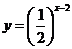 的图象的交点为
的图象的交点为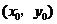 ,则
,则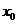 所在的区间是_____________.
所在的区间是_____________.
3.下列大小关系正确的是_____________.
①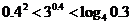 ;②
;②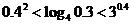 ;③
;③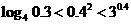 ;
;
④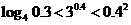
2.把函数y=ex的图象按向量a=(2,3)平移,得到y=f(x)的图象,则f(x)=_________.
1.函数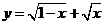 的定义域为_______________.
的定义域为_______________.
22.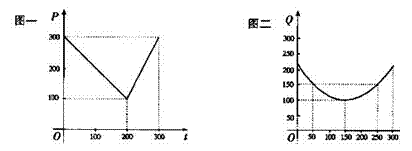 某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示。
某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示。
(Ⅰ)写出图一表示的市场售价与时间的函数关系式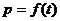 ;
;
写出图二表示的种植成本与时间的函数关系式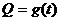 ;
;
(Ⅱ)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?
(注:市场售价各种植成本的单位:元/102㎏,时间单位:天)
21.已知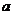 是实数,函数
是实数,函数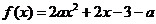 .如果函数
.如果函数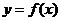
在区间[-1,1]上有零点,求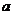 的取值范围.
的取值范围.
19.已知定义域为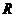 的函数
的函数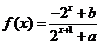 是奇函数。 (Ⅰ)求
是奇函数。 (Ⅰ)求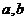 的值;
的值;
(Ⅱ)若对任意的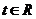 ,不等式
,不等式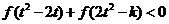 恒成立,求
恒成立,求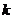 的取值范围;
的取值范围;
20 .已知函数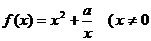 ,常数
,常数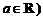 .
.
(1)讨论函数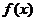 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若函数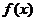 在
在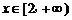 上为增函数,求
上为增函数,求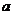 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com