19.(本题满分13分)

已知椭圆的左、右焦点分别为F₁、F₂，短轴端点分别为A、B，且四边形F₁AF₂B是边长为2的正方形

　(I)求椭圆的方程；

　(II)若C、D分别是椭圆长轴的左、右端点，动点M满足，连结CM交椭圆于P，证明为定值(O为坐标原点)；_K^S*5U.C#O%

　(III)在(II)的条件下，试问在x轴上是否存在异于点C的定点Q，使以线段MP为直径的圆恒过直线DP、MQ的交点，若存在，求出Q的坐标，若不存在，说明理由

18.(本题满分13分)

某投资公司在2010年年初准备将1000万元投资到“低碳”项目上，现有两个项目供选择：

项目一：新能源汽车．据市场调研，投资到该项目上，到年底可能获利，也可能亏损，且这两种情况发生的概率分别为和；

项目二：通信设备．据市场调研，投资到该项目上，到年底可能获利，可能亏损，也可能不赔不赚，且这三种情况发生的概率分别为、和

(Ⅰ)针对以上两个投资项目，请你为投资公司选择一个合理的项目，并说明理由；

(Ⅱ)若市场预期不变，该投资公司按照你选择的项目长期投资(每一年的利润和本金继续用作投资)，问大约在哪一年的年底总资产(利润+本金)可以翻一番？

(参考数据：，)

17．(本小题满分13分)

如图的多面体是底面为平行四边形的直四棱柱ABCD-，经平面AEFG

所截后得到的图形．其中∠BAE=∠GAD=45°，AB=2AD=2，∠BAD=60

(I)求证：BD⊥平面ADG；(Ⅱ)求平面AEFG与平面ABCD所成锐二面角的余弦值．

16.(本题满分13分)

已知＝(cosx+sinx，sinx)，＝(cosx－sinx，2cosx)，

(Ⅰ)求证：向量与向量不可能平行；(Ⅱ)若f(x)＝·，且x∈[－,]时，求函数f(x)的最大值及最小值

15．随着科学技术的不断发展，人类通过计算机已找到了630万位的最大质数。陈成在学习中发现由41，43，47，53，61，71，83，97组成的数列中每一个数都是质数，他根据这列数的一个通项公式，得出了数列的后几项，发现它们也是质数。于是他断言：根据这个通项公式写出的数均为质数。请你写出这个通项公式　　　　　　　　　　　 ，从这个通项公式举出一个反例，说明陈成的说法是错误的：　　　　　 　　　　　　　　　　.

14．按如图所示的程序框图运算，若输出，则输入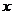的取值范围是______

13．如图，是某几何体的三视图，其中正视图是腰长为的等腰三角形俯视图

是半径为的半圆，则该几何体的表面积是　 　　　．

12．设0＜θ＜，已知，,猜想＝________．

11．的二项展开式中，常数项的值是　　　　 .

10．将一颗骰子投掷两次，第一次出现的点数记为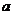，第二次出现的点数记为,

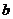设两条直线l₁：ax+by＝2，l₂：x+2y＝2平行的概率为P₁，相交的概率为P₂，

试问点(P₁，P₂)与直线l₂：x+2y＝2的位置关系是(　　 )

　　 A．P在直线l₂的右下方　　　　　　　　　 B．P在l₂直线的左下方

　　 C．P在直线l₂的右上方　　　　　　　　　 D．P在直线l₂上