
1、课文题目是《奥斯维辛没有什么新闻》,那么,奥斯维辛到底是一个什么地方呢?请看课文第3段。
(学生讨论,教师点拨,下同)
答案要点:奥斯维辛是波兰南方的一个城市,二战期间纳粹德国在这里建立了最大的集中营,被称为二战期间纳粹德国最大的“杀人工厂”,据统计报道有400万人在这里遭到杀害。
今天我们来学习第10课《短新闻两篇》第二篇《奥斯维辛没有什么新闻》,《奥斯维辛没有什么新闻》这篇文章由美国记者罗森塔尔撰写,发表之后立即引起了强烈反响,各大报纸争相转载,并获得了美国普利策新闻奖,成为新闻史上的佳作。这是一篇什么样的新闻呢?请大家看课文。(板书课题)
22.(14分)
设椭圆E: 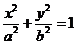 (a,b>0)过M(2,
(a,b>0)过M(2,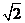 ) ,N(
) ,N(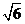 ,1)两点,O为坐标原点.
,1)两点,O为坐标原点.
(Ⅰ)求椭圆E的方程;
(Ⅱ)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,
且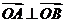 ?若存在,写出该圆的方程,并求|AB
|的取值范围,若不存在说明理
?若存在,写出该圆的方程,并求|AB
|的取值范围,若不存在说明理
21.(12分)如图,已知椭圆的中心在原点,焦点在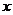 轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在
轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线l在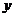 轴上的截距为
轴上的截距为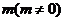 ,l交椭圆于A、B两个不同点.
,l交椭圆于A、B两个不同点.
(1)求椭圆的方程;
(2)求m的取值范围;
(3)求证直线MA、MB与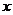 轴始终围成一个等腰三角形.
轴始终围成一个等腰三角形.
20.(12分)
已知椭圆G的中心在坐标原点,长轴在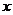 轴上,离心率为
轴上,离心率为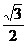 ,两个焦点分别为
,两个焦点分别为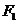 和
和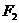 ,椭
,椭
圆G上一点到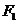 和
和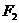 的距离之和为12.圆
的距离之和为12.圆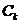 :
: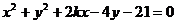
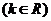 的圆心为点
的圆心为点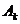 .
.
(1)求椭圆G的方程
(2)求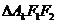 的面积
的面积
(3)问是否存在圆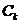 包围椭圆G?请说明理由.
包围椭圆G?请说明理由.
19.(12分)双曲线的中心为原点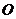 ,焦点在
,焦点在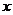 轴上,两条渐近线分别为
轴上,两条渐近线分别为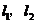 ,经过右焦点
,经过右焦点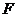 垂直于
垂直于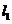 的直线分别交
的直线分别交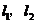 于
于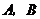 两点.已知
两点.已知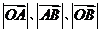 成等差数列,且
成等差数列,且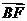 与
与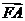 同向.
同向.
(Ⅰ)求双曲线的离心率;
(Ⅱ)设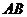 被双曲线所截得的线段的长为4,求双曲线的方程.
被双曲线所截得的线段的长为4,求双曲线的方程.
18.(12分)已知一动圆M,恒过点F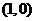 ,且总与直线
,且总与直线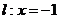 相切.
相切.
(Ⅰ)求动圆圆心M的轨迹C的方程;
(Ⅱ)探究在曲线C上,是否存在异于原点的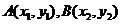 两点,当
两点,当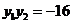 时,
时,
直线AB恒过定点?若存在,求出定点坐标;若不存在,说明理由.
17.(12分)设O是坐标原点,F是抛物线y2=2px(p>0)的焦点,A是抛物线上的一个动点,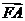 与x轴正方向的夹角为600,求|
与x轴正方向的夹角为600,求|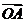 |的值.
|的值.
16.已知两个点M(-5,0)和N(5,0),若直线上存在点P,使|PM|-|PN|=6,则称该直线为“B型直线”,给出下列直线:①y=x+1; ②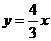 ;③y=2;④y=2x+1.其中为“B型直线”的是
.(填上所有正确结论的序号)
;③y=2;④y=2x+1.其中为“B型直线”的是
.(填上所有正确结论的序号)
15.已知两条直线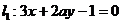 ,
,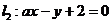 ,若
,若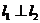 ,则
,则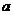 =___ ____。
=___ ____。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com