
5.给出下列问题:
①有10个车站,共需要准备多少种车票?
②有10个 车站,共有多少中不同的票价?
车站,共有多少中不同的票价?
③平面内有10个点,共可作出多少条不同的有向线段?
④有10个同学,假期约定每两人通电话一次,共需通话多少次?
⑤从10个同学中选出2名分别参加数学和物理竞赛,有多少中选派方法?
以上问题中,属于排列问题的是(填写问题的编号).
4.5人站成一排照相,甲不站在排头的排法有( )
 .24种
.24种 .72种
.72种 .96种
.96种 .120种
.120种
3. 且
且 则
则 用排列数符号表示为( )
用排列数符号表示为( )
 .
.
 .
.
 .
.
 .
.
2.信号兵用3种不同颜色的旗子各一面,每次打出3面,最多能打出不同的信号有( )
 .3种
.3种 .6种
.6种 .1种
.1种 .27种
.27种
1.四支足球队争夺冠、亚军,不同的结果有( )
 .
. 种
种 .10种
.10种 .12种
.12种 .16种
.16种
例1.计算:(1) ;(2)
;(2) ;(3)
;(3) .
.
解:(1) =
= =3360;
=3360;
(2) =
= =720;
=720;
(3) =
= =360.
=360.
例2.(1)若 ,则
,则 ,
, .
.
(2)若 则
则 用排列数符号表示.
用排列数符号表示.
解:(1) 17,
17, 14.
14.
(2)若 则
则 =
= .
.
例3.(1)从 这五个数字中,任取2个数字组成分数,不同值的分数共有多少个?
这五个数字中,任取2个数字组成分数,不同值的分数共有多少个?
(2)5人站成一排照相,共有多少种不同的站法?
(3)某年全国足球甲级(A组)联赛共有14队参加,每队都要与其余各队在主客场分别比赛1次,共进行多少场比赛?
解:(1) ;
;
(2) ;
;
(3) .
.
4.排列数公式及其推导:
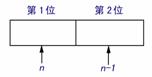
由 的意义:假定有排好顺序的2个空位,从
的意义:假定有排好顺序的2个空位,从 个元素
个元素 中任取2个元素去填空,一个空位填一个元素,每一种填法就得到一个排列,反过来,任一个排列总可以由这样的一种填法得到,因此,所有不同的填法的种数就是排列数
中任取2个元素去填空,一个空位填一个元素,每一种填法就得到一个排列,反过来,任一个排列总可以由这样的一种填法得到,因此,所有不同的填法的种数就是排列数 .由分步计数原理完成上述填空共有
.由分步计数原理完成上述填空共有 种填法,
种填法,
∴ =
= .
.
由此,求 可以按依次填3个空位来考虑,∴
可以按依次填3个空位来考虑,∴ =
= ,
,
求 以按依次填
以按依次填 个空位来考虑
个空位来考虑 ,
,
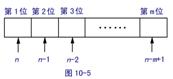 排列数公式:
排列数公式:
 (
( )
)
说明:(1)公式特征:第一个因数是 ,后面每一个因数比它前面一个
,后面每一个因数比它前面一个
少1,最后一个因数是 ,共有
,共有 个因数;
个因数;
(2)全排列:当 时即
时即 个不同元素全部
个不同元素全部 取出的一个排列.
取出的一个排列.
全排列数: (叫做n的阶乘).
(叫做n的阶乘).
3.排列数的定义:
从 个不同元素中,任取
个不同元素中,任取 (
( )个元素的所有排列的个数叫做从
)个元素的所有排列的个数叫做从 个元素中取出
个元素中取出 元素的排列数,用符号
元素的排列数,用符号 表示.
表示.
 注意区别排列和排列数的不同:“一个排列”是指:
注意区别排列和排列数的不同:“一个排列”是指: 从
从 个不同元素中,任取
个不同元素中,任取
 个元素按照一定的顺序排成一列,不是数;“排列数”是指从
个元素按照一定的顺序排成一列,不是数;“排列数”是指从 个不同元素中,任取
个不同元素中,任取 (
( )个元素的所有排列的个数,是一个数.所以符号
)个元素的所有排列的个数,是一个数.所以符号 只表示排列数,而不表示具体的排列.
只表示排列数,而不表示具体的排列.
2.排列的概念 :
:
从 个不同元素中,任取
个不同元素中,任取 (
( )个元素(这里的被取元素各
)个元素(这里的被取元素各 不相同)按照
不相同)按照 一定的顺序排成一列,叫做从
一定的顺序排成一列,叫做从 个不同元素中取出
个不同元素中取出 个元素的一个排列.
个元素的一个排列.
说明:(1)排列的定义包括两个方面:①取出元素,②按一定的顺序排列;
(2)两个排列相同的条件:①元素完全相同,②元素的排列顺序也相同.
1.问题:
问题1.从甲、乙、丙3名同学中选取2名同学参加某一天的一项活动,其中一名同学参加上午的活动,一名同学参加下午的活动,有多少种不同的方法?
分析:这个问题就是从甲、乙、丙3名同学中每次选取2名同学,按照参加上午的活动在前,参加下午活动在后的顺序排列,一共有多少种不同的排法的问题,共有6种不同的排法:甲乙甲丙乙甲乙丙丙甲丙乙,其中被取的对象叫做元素.
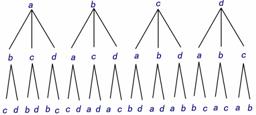
问题2.从 这四个字母中,每次取出3个按顺序排成一列,共有多少种不同的排法?
这四个字母中,每次取出3个按顺序排成一列,共有多少种不同的排法?
分析:解决这个问题分三个步骤:第一步先确定左边的字母,在4个字母中任取1个,有4种方法;第二步确定中间的字母,从余下的3个字母中取,有3种方法;第三步确定右边的字母,从余下的2个字母中取,有2种方法.
由分步计数原理共有:4×3×2=24种不同 的方法,用树型图排出,并写出所有的排列.由此可写出所有的排法.
的方法,用树型图排出,并写出所有的排列.由此可写出所有的排法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com