
1. ⑴复数的单位为i,它的平方等于-1,即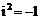 .
.
⑵复数及其相关概念:
①
复数-形如a + bi的数(其中 );
);
②
实数-当b = 0时的复数a + bi,即a;
③
虚数-当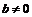 时的复数a + bi;
时的复数a + bi;
④
纯虚数-当a = 0且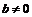 时的复数a + bi,即bi.
时的复数a + bi,即bi.
⑤
复数a + bi的实部与虚部-a叫做复数的实部,b叫做虚部(注意a,b都是实数)
⑥
复数集C-全体复数的集合,一般用字母C表示.
⑶两个复数相等的定义:
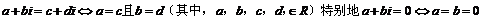 .
.
⑷两个复数,如果不全是实数,就不能比较大小.
注:①若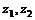 为复数,则
为复数,则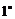 若
若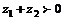 ,则
,则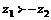 .(×)[
.(×)[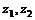 为复数,而不是实数]
为复数,而不是实数]
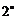 若
若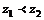 ,则
,则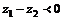 .(√)
.(√)
②若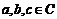 ,则
,则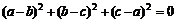 是
是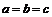 的必要不充分条件.(当
的必要不充分条件.(当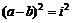 ,
,
 时,上式成立)
时,上式成立)
20..(2008陕西文)已知数列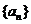 的首项
的首项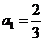 ,
,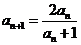 ,
,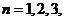 ….
….
(Ⅰ)证明:数列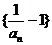 是等比数列; (Ⅱ)数列
是等比数列; (Ⅱ)数列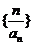 的前
的前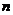 项和
项和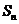 .
.
19.(2000广东)设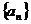 为等比数列,
为等比数列,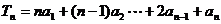 ,已知
,已知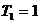 ,
,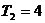 。
。
(Ⅰ)求数列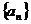 的首项和通项公式; (Ⅱ)求数列
的首项和通项公式; (Ⅱ)求数列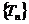 的通项公式。
的通项公式。
18.(2002广东、河南、江苏)设{an}为等差数列,{bn}为等比数列,a1=b1 =1, a2+a4 =b3,
b2b4=a3.分别求出{an}及{bn}的前10项的和S10及T10.
17.(2004全国Ⅳ卷文) 已知数列{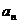 }为等比数列,
}为等比数列,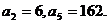
(Ⅰ)求数列{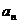 }的通项公式; (Ⅱ)设
}的通项公式; (Ⅱ)设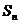 是数列{
是数列{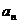 }的前
}的前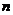 项和,证明
项和,证明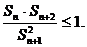
16.(2007全国Ⅱ文) 设等比数列 {an}的公比q<1,前n项和为Sn.已知a3=2,S4=5S2,求{an}的通项公式.
15.(2006全国Ⅰ卷文)已知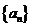 为等比数列,
为等比数列,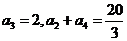 ,求
,求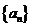 的通项式。
的通项式。
14.(2002北京文、理)等差数列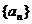 中,a1=2,公差不为零,且a1,a3,a11 恰好是某等比数列的前三项,那么该等比数列公比的值等于_______________________.
中,a1=2,公差不为零,且a1,a3,a11 恰好是某等比数列的前三项,那么该等比数列公比的值等于_______________________.
13.(2005湖北理)设等比数列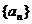 的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为 .
的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为 .
12.(2004全国Ⅰ卷文)已知等比数列{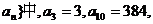 则该数列的通项
则该数列的通项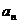 =
.
=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com