
某一分子离子提供孤对电子, 提供空轨道形成的特殊一种的 叫配位键,通常把 的化合物称为配位化合物,简称配合物,过渡金属易形成配物。
杂化轨道理论要点:
①只有 原子轨道才能杂化
②原子轨道杂化时,轨道 不变,轨道的形状发生变化
③原子轨道杂化后总能量比原有轨道能量之和降低
④杂化轨道只于形成δ键
⑤sp杂化轨道夹角 ,sp2杂化轨道夹角 ,sp3杂化轨道夹角 。
思考:怎样判断有几个轨道参与了杂化?
价层电子对互斥模型把分子分成两大类:一类是 ,如CO2、CH4等,其立体结构可用 周围的原子数n来预测,如ABn,n=2, 形,n=3, 形,n=4, 形;另一类是 的分子。
补充:1 已知: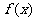 =x
=x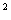 -x+3 求: f(x+1), f(
-x+3 求: f(x+1), f(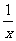 )
)
解:f(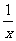 )=(
)=(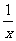 )
)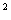 -
-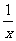 +3;
+3;
f(x+1)=(x+1)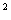 -(x+1)+3=x
-(x+1)+3=x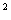 +x+3
+x+3
2
已知函数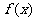 =4x+3,g(x)=x
=4x+3,g(x)=x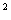 ,求f[f(x)],f[g(x)],g[f(x)],g[g(x)].
,求f[f(x)],f[g(x)],g[f(x)],g[g(x)].
解:f[f(x)]=4f(x)+3=4(4x+3)+3=16x+15;
f[g(x)]=4g(x)+3=4x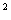 +3;
+3;
g[f(x)]=[f(x)]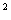 =(4x+3)
=(4x+3)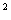 =16x
=16x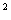 +24x+9;
+24x+9;
g[g(x)]=[g(x)]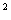 =(x
=(x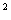 )
)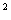 =x
=x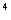 .
.
3 若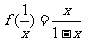 求f(x)
求f(x)
解: 令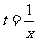 则
则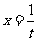 (t¹0) 则
(t¹0) 则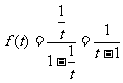
∴f(x)=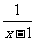 (x¹0且x¹1)
(x¹0且x¹1)
区间的概念和记号,求函数定义域的基本方法,求解析式的方法,分段函数;复合函数
3.若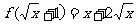 ,求f(x)
,求f(x)
解法一(换元法):令t=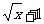 则x=t
则x=t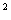 -1, t≥1代入原式有
-1, t≥1代入原式有

∴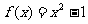 (x≥1)
(x≥1)
解法二(定义法):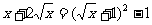
∴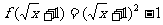
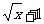 ≥1
≥1
∴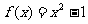 (x≥1)
(x≥1)
2.已知f(x)是一次函数, 且f[f(x)]=4x-1, 求f(x)的解析式
解:设f(x)=kx+b则 k(kx+b)+b=4x-1
则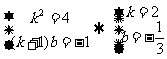 或
或 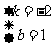
∴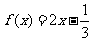 或
或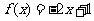
1.设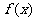 的定义域是[-3,
的定义域是[-3,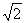 ],求函数
],求函数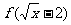 的定义域
的定义域
解:要使函数有意义,必须: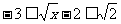 得:
得: 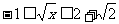
∵ 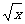 ≥0 ∴
≥0 ∴ 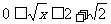
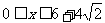
∴
函数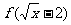 的定域义为:
的定域义为: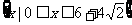
例1已知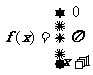
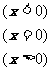

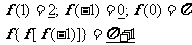
例2已知f(x)=x2-1 g(x)=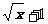 求f[g(x)]
求f[g(x)]
解:f[g(x)]=(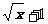 )2-1=x+2
)2-1=x+2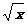
例3 求下列函数的定义域:
①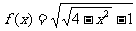 ②
②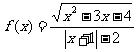
③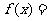
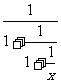 ④
④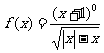
⑤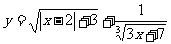
解:①要使函数有意义,必须: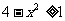 即:
即: 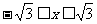
∴函数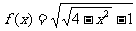 的定义域为: [
的定义域为: [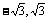 ]
]
②要使函数有意义,必须: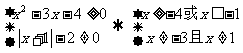
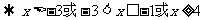
∴定义域为:{ x|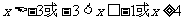 }
}
③要使函数有意义,必须: 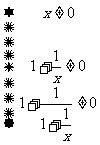 Þ
Þ 
∴函数的定义域为: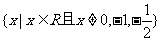
④要使函数有意义,必须: 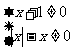

∴定义域为: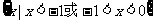
⑤要使函数有意义,必须: 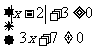

即 x<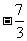 或 x>
或 x>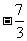 ∴定义域为:
∴定义域为: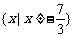
例4 若函数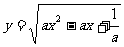 的定义域是R,求实数a 的取值范围
的定义域是R,求实数a 的取值范围
解:∵定义域是R,∴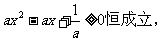
∴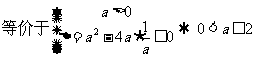
例5 若函数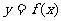 的定义域为[-1,1],求函数
的定义域为[-1,1],求函数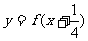
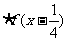 的定义域
的定义域
解:要使函数有意义,必须:
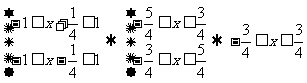
∴函数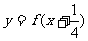
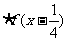 的定义域为:
的定义域为: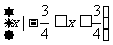
求用解析式y=f(x)表示的函数的定义域时,常有以下几种情况:
①若f(x)是整式,则函数的定义域是实数集R;
②若f(x)是分式,则函数的定义域是使分母不等于0的实数集;
③若f(x)是二次根式,则函数的定义域是使根号内的式子大于或等于0的实数集合;
④若f(x)是由几个部分的数学式子构成的,则函数的定义域是使各部分式子都有意义的实数集合;
⑤若f(x)是由实际问题抽象出来的函数,则函数的定义域应符合实际问题.
例6 已知f(x)满足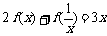 ,求
,求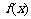 ;
;
∵已知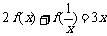 ①,
①,
将①中x换成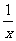 得
得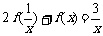 ②,
②,
①×2-②得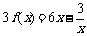 ∴
∴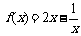 .
.
例7 设二次函数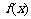 满足
满足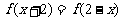 且
且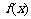 =0的两实根平方和为10,图象过点(0,3),求
=0的两实根平方和为10,图象过点(0,3),求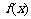 的解析式.
的解析式.
解:设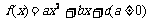 ,
,
∵图象过点(0,3),∴有f(0)=c=3,故c=3;
又∵f(x)满足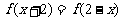 且
且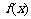 =0的两实根平方和为10,
=0的两实根平方和为10,
∴得对称轴x=2且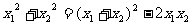 =10,
=10,
即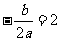 且
且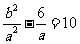 ,∴a=1,b=-4,∴
,∴a=1,b=-4,∴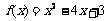
4.复合函数:设 f(x)=2x-3,g(x)=x2+2,则称 f[g(x)] =2(x2+2)-3=2x2+1(或g[f(x)] =(2x-3)2+2=4x2-12x+11)为复合函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com