
5、要理解“充要条件”的概念,对于符号“ ”要熟悉它的各种同义词语
”要熟悉它的各种同义词语 “等价于”,“当且仅当”,“必须并且只需”,“……,反之也真”等
“等价于”,“当且仅当”,“必须并且只需”,“……,反之也真”等
4、.要理解“充分条件”“必要条件”的概念,当“若p则q”形式的命题为真时,就记作p q,称p是q的充分条件,同时称q是p的必要条件,因此判断充分条件或必要条件就归结为判断命题的真假
q,称p是q的充分条件,同时称q是p的必要条件,因此判断充分条件或必要条件就归结为判断命题的真假
3、当p和q互为充要时,体现了命题等价转换的思想。
2、在判断充分条件及必要条件时,首先要分清哪个命题是条件,哪个命题是结论,其次,结论要分四种情况说明:充分不必要条件,必要不充分条件,充分且必要条件,既不充分又不必要条件。从集合角度看,若记满足条件p的所有对象组成集合A,满足条件q的所有对象组成集合q,则当A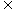 B时,p是q的充分条件。B
B时,p是q的充分条件。B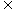 A时,p是q的充分条件。A=B时,p是q的充要条件;
A时,p是q的充分条件。A=B时,p是q的充要条件;
1、定义:对命题“若p则q”而言,当它是真命题时,p是q的充分条件,q是p的必要条件,当它的逆命题为真时,q是p的充分条件,p是q的必要条件,两种命题均为真时,称p是q的充要条件;
4.常见词语的否定如下表所示:
|
词语 |
是 |
一定是 |
都是 |
大于 |
小于 |
|
词语的否定 |
不是 |
一定不是 |
不都是 |
小于或等于 |
大于或等于 |
|
词语 |
且 |
必有一个 |
至少有n个 |
至多有一个 |
所有x成立 |
|
词语的否定 |
或 |
一个也没有 |
至多有n-1个 |
至少有两个 |
存在一个x不成立 |
例8、(2007山东)命题“对任意的 ”的否定是( )
”的否定是( )
A.不存在 B.存在
B.存在
C.存在 D. 对任意的
D. 对任意的
解:命题的否定与否命题不同,命题的否定是将全称量词改为特称量词,或将特称量词改为全称量词,再否定结论即可,故选(C)。
例9、命题“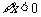 ,有
,有 ”的否定是
.
”的否定是
.
解:将“存在”改为“任意”,再否定结论,注意存在与任意的数学符号表示法,答案:
考点5、充分条件与必要条件
2.全称命题与特称命题
(1)全称命题:含有全称量词的命题。“对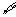 x
x M,有p(x)成立”简记成“
M,有p(x)成立”简记成“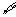 x
x M,p(x)”。
M,p(x)”。
(2)特称命题:含有存在量词的命题。“ x
x M,有p(x)成立” 简记成“
M,有p(x)成立” 简记成“ x
x M,p(x)”。3. 同一个全称命题、特称命题,由于自然语言的不同,可以有不同的表述方法,现列表如下,供参考。
M,p(x)”。3. 同一个全称命题、特称命题,由于自然语言的不同,可以有不同的表述方法,现列表如下,供参考。
|
命题 |
全称命题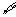 x x M,p(x) M,p(x) |
特称命题 x x M,p(x) M,p(x) |
|
表述 方法 |
①所有的x M,使p(x)成立 M,使p(x)成立 |
①存在x M,使p(x)成立 M,使p(x)成立 |
②对一切x M,使p(x)成立 M,使p(x)成立 |
②至少有一个x M,使p(x)成立 M,使p(x)成立 |
|
③对每一个x M,使p(x)成立 M,使p(x)成立 |
③对有些x M,使p(x)成立 M,使p(x)成立 |
|
④任给一个x M,使p(x)成立 M,使p(x)成立 |
④对某个x M,使p(x)成立 M,使p(x)成立 |
|
⑤若x M,则p(x)成立 M,则p(x)成立 |
⑤有一个x M,使p(x)成立 M,使p(x)成立 |
1.全称量词与存在量词
(1)全称量词:对应日常语言中的“一切”、“任意的”、“所有的”、“凡是”、“任给”、“对每一个”等词,用符号“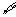 ”表示。
”表示。
(2)存在量词:对应日常语言中的“存在一个”、“至少有一个”、“有个”、“某个”、“有些”、“有的”等词,用符号“ ”表示。
”表示。
4、四种命题:记“若q则p”为原命题,则否命题为“若非p则非q”,逆命题为“若q则p“,逆否命题为”若非q则非p“。其中互为逆否的两个命题同真假,即等价。因此,四种命题为真的个数只能是偶数个。
例6、(2008广东高考)命题“若函数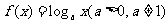 在其定义域内是减函数,则
在其定义域内是减函数,则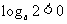 ”的逆否命题是( )
”的逆否命题是( )
A、若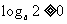 ,则函数
,则函数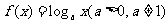 在其定义域内不是减函数
在其定义域内不是减函数
B、若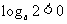 ,则函数
,则函数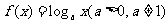 在其定义域内不是减函数
在其定义域内不是减函数
C、若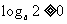 ,则函数
,则函数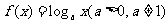 在其定义域内是减函数
在其定义域内是减函数
D、若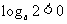 ,则函数
,则函数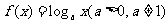 在其定义域内是减函数
在其定义域内是减函数
解:逆否命题是将原命题的结论的否定作为条件,原命题的条件的否定作为结论,故应选(A)。
例7、已知命题 方程
方程 有两个不相等的负数根;
有两个不相等的负数根;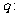 方程
方程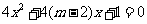 无实根.若“
无实根.若“ 或
或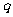 ”为真,“
”为真,“ 且
且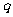 ”为假,求实数
”为假,求实数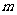 的取值范围.
的取值范围.
解: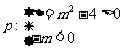
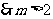 .
.
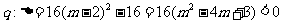 ,
,
 .
.
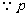 或
或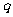 为真,
为真, 且
且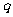 为假,
为假,
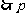 真,
真,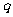 假或
假或 假,
假,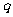 真.
真.
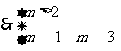 或
或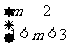 ,故
,故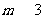 或
或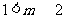 .
.
考点4、全称量词与存在量词
3、复合命题的真假:对p且q而言,当q、p为真时,其为真;当p、q中有一个为假时,其为假。对p或q而言,当p、q均为假时,其为假;当p、q中有一个为真时,其为真;当p为真时,非p为假;当p为假时,非p为真。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com