
4、[解析]:由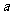 >b且c>d
>b且c>d
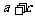 >b+d,而由
>b+d,而由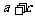 >b+d
>b+d 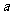 >b且c>d,可举反例。选A
>b且c>d,可举反例。选A
3、[解析]由 得
得 ,选B
,选B
2、[解析]集合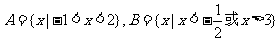 ,∴
,∴ 选D
选D
1-10. BDBAB CACAD
1、[解析] 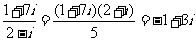 ,∴
,∴ ,选B。
,选B。
(16)(本小题满分12分)
在△ABC中,sin(C-A)=1,sinB=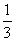 .
.
(Ⅰ)求sinA的值;
(Ⅱ)设AC=,求△ABC的面积. 

(17)(本小题满分12分)
某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区,B肯定是受A感染的。对于C,因为难以判定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是1/2.同样也假设D受A、B和C感染的概率都是1/3.在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量。写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望)。
(18)(本小题满分13分)
如图,四棱椎F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=.AE、CF都与平面ABCD垂直,AE=1,CF=2.
(Ⅰ) 求二面角B-AF-D的大小;
(Ⅱ) 求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积。 

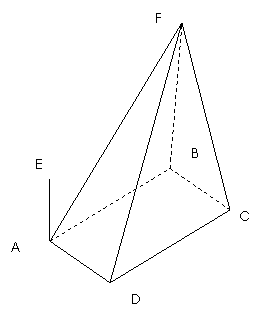
第(18)题图
(19)(本小题满分12分)
已知函数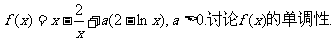


(20)(本小题满分13分)
点P(x0,y0)在椭圆 1(a>b>0)上,x0=
1(a>b>0)上,x0= , y0=
, y0=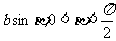 . 直线
. 直线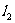 与直线
与直线 :
: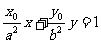 垂直,O为坐标原点,直线OP的倾斜角为
垂直,O为坐标原点,直线OP的倾斜角为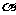 ,直线
,直线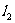 的倾斜角为
的倾斜角为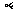 .
.
(Ⅰ)证明:点P是椭圆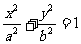 与直线
与直线 的唯一交点;
的唯一交点;
(Ⅱ)证明:tan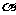 ,tan
,tan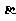 ,tan
,tan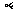 构成等比数列。
构成等比数列。
(21)(本小题满分13分)
首项为正数的数列{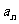 }满足
}满足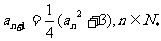 .
.
(Ⅰ)证明:若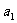 为奇数,则对一切
为奇数,则对一切 ,
,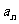 都是奇数;
都是奇数;
(Ⅱ)若对一切 ,都有
,都有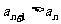 ,求
,求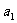 的取值范围。
的取值范围。
W数学(理科)试题 第4页(共4页) 

2009年普通高等学校招生全国统一考试(安徽卷)
数学(理科)
(11)若随机变量X~N(μ,σ2),则P(X≤μ)= .
(12)以直角坐标系的原点为极点,x轴的正半轴为极轴, 

并在两种坐标系中取相同的长度单位,已知直线的
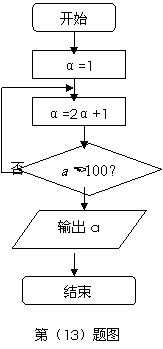 极坐标方程为
极坐标方程为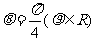 ,它与曲线
,它与曲线
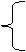

(α为参数)相交于两点A和B,则

|AB|= .
(13)程序框图(即算法流程图)如图所示,其输出结果是
.
(14)给定两个长度为1的平面向量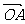 和
和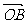 ,它们的夹
,它们的夹
角为120°.如图所示,点C在以O为圆心的圆弧
上变动.若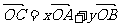 ,其中
,其中 ,则x+y
,则x+y
的最大值是 .
 (15)对于四面体ABCD,下列命题正确的是
(15)对于四面体ABCD,下列命题正确的是
(写出所有正确命题的编号).
①相对棱AB与CD所在的直线异面;
②由顶点A作四面体的高,其垂足是△BCD三条高线的交点;
③若分别作△ABC和△ABD的边AB上的高,则这两条高所在的直线异面;
④分别作三组相对棱中点的连线,所得的三条线段相交于一点;
⑤最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱.
(1)i是虚数单位,若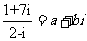 (a、b∈R),则乘积ab的值是
(a、b∈R),则乘积ab的值是
(A)-15 (B)-3 (C)3 (D)15
(2)若集合A={x|︱2x-1︱<3},B={x|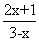 <0},则A∩B是
<0},则A∩B是
(A){x|-1<x< 或2<x<3}
(B){x|2<x<3}
或2<x<3}
(B){x|2<x<3}
(C){x| <x<2}
(D){x|-1<x<
<x<2}
(D){x|-1<x< }
}
 (3)下列曲线中离心率为
(3)下列曲线中离心率为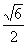 的是
的是
(A)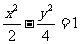 (B)
(B)
(C)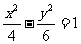 (D)
(D)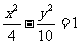

(4)下列选项中, 是
是 的必要不充分条件的是
的必要不充分条件的是
(A)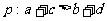 ,
, 
(B)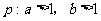 ,
, 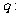
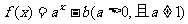 的图像不过第二象限
的图像不过第二象限
(C) ,
,
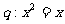
(D) ,
,
 在
在 上为增函数
上为增函数
(5)已知 为等差数列,
为等差数列,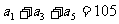 ,
,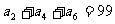 。以
。以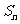 表示
表示 的前n项和,则使得
的前n项和,则使得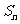 达到最大值的n是
达到最大值的n是
(A)21 (B)20 (C)19 (D)18
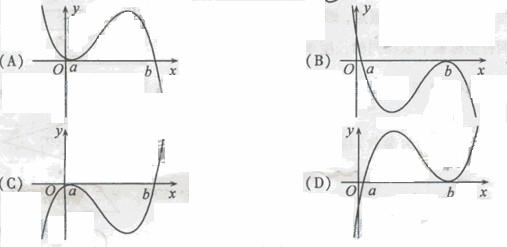
(6)设 ,函数
,函数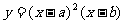 的图像可能是
的图像可能是
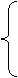

(7)若不等式组
 所表示的平面区域被直线
所表示的平面区域被直线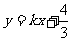 分为面积相等的两
分为面积相等的两

部分,则k的值是
(A) (B)
(B)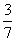 (C)
(C) (D)
(D)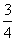
(8)已知函数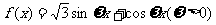 ,
, 的图像与直线
的图像与直线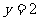 的两个相邻交点的距离等于
的两个相邻交点的距离等于 ,则
,则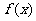 的单调递增区间是
的单调递增区间是
(A)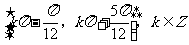 (B)
(B)
(C)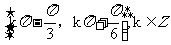 (D)
(D)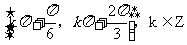
(9)已知函数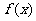 在R上满足
在R上满足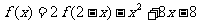 ,则曲线
,则曲线 在点
在点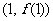 处的切线方程是
处的切线方程是
(A)
 (B)
(B)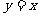 (C)
(C)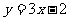 (D)
(D)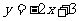
(10)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点种任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于
(A)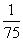 (B)
(B)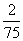 (C)
(C)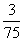 (D)
(D)
(在此卷上答题无效)
2009年普通高等学校招生全国统一考试(安徽卷)
数 学(理科)
第Ⅱ卷(非选择题 共100分)
请用0.5毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效.
22. (本小题满分14分)
设数列 的前
的前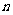 项和为
项和为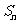 ,对任意的正整数
,对任意的正整数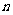 ,都有
,都有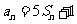 成立,记
成立,记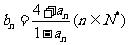 。
。 

(I)求数列 与数列
与数列 的通项公式;
的通项公式;
(II)设数列 的前
的前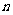 项和为
项和为 ,是否存在正整数
,是否存在正整数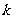 ,使得
,使得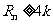 成立?若存在,找出一个正整数
成立?若存在,找出一个正整数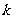 ;若不存在,请说明理由;
;若不存在,请说明理由;
(III)记 ,设数列
,设数列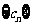 的前
的前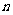 项和为
项和为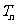 ,求证:对任意正整数
,求证:对任意正整数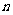 都有
都有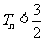 ;
;
[解析](I)当 时,
时,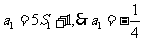


又
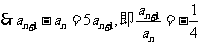
∴数列 是首项为
是首项为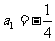 ,公比为
,公比为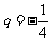 的等比数列,
的等比数列,
∴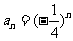 ,
, …………………………………3分
…………………………………3分
(II)不存在正整数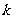 ,使得
,使得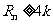 成立。
成立。
证明:由(I)知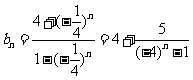


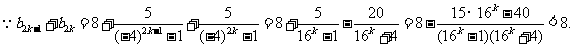
∴当n为偶数时,设


∴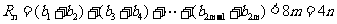
当n为奇数时,设
∴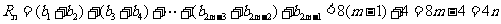
∴对于一切的正整数n,都有


∴不存在正整数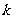 ,使得
,使得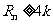 成立。 …………………………………8分
成立。 …………………………………8分
(III)由 得
得 

 又
又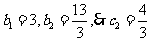 ,
, 

当 时,
时, ,
,
当 时,
时,
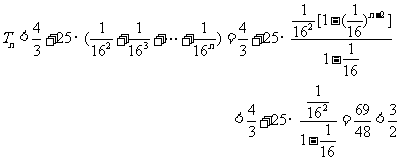


…………………………………14分

21. (本小题满分12分) 

已知椭圆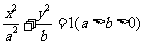 的左、右焦点分别为
的左、右焦点分别为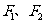 ,离心率
,离心率 ,右准线方程为
,右准线方程为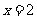 。
。
(I)求椭圆的标准方程;
(II)过点 的直线
的直线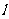 与该椭圆交于
与该椭圆交于 两点,且
两点,且 ,求直线
,求直线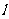 的方程。
的方程。
[解析](I)由已知得 ,解得
,解得


∴ 
∴ 所求椭圆的方程为 …………………………………4分
…………………………………4分
(II)由(I)得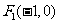 、
、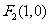
①若直线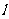 的斜率不存在,则直线
的斜率不存在,则直线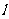 的方程为
的方程为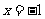 ,由
,由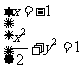 得
得
设 、
、 ,
, 

∴ 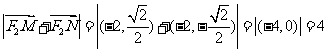 ,这与已知相矛盾。
,这与已知相矛盾。
②若直线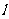 的斜率存在,设直线直线
的斜率存在,设直线直线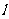 的斜率为
的斜率为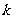 ,则直线
,则直线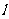 的方程为
的方程为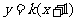 ,
,
设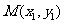 、
、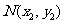 ,
,
联立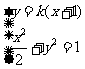 ,消元得
,消元得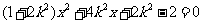
∴ 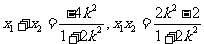 ,
,
∴ 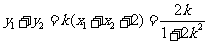 ,
, 

又∵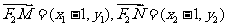
∴ 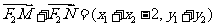
∴ 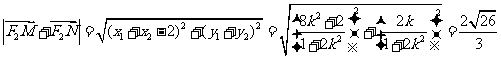
化简得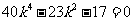
解得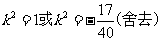
∴ 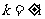
∴ 所求直线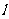 的方程为
的方程为 …………………………………12分
…………………………………12分
18. (本小题满分12分)
为振兴旅游业,四川省2009年面向国内发行总量为2000万张的熊猫优惠卡,向省外人士发行的是熊猫金卡(简称金卡),向省内人士发行的是熊猫银卡(简称银卡)。某旅游公司组织了一个有36名游客的旅游团到四川名胜旅游,其中 是省外游客,其余是省内游客。在省外游客中有
是省外游客,其余是省内游客。在省外游客中有 持金卡,在省内游客中有
持金卡,在省内游客中有 持银卡。
持银卡。 

(I)在该团中随机采访2名游客,求恰有1人持银卡的概率;
(II)在该团中随机采访2名游客,求其中持金卡与持银卡人数相等的概率.
[解析]I)由题意得,省外游客有27人,其中9人持金卡;省内游客有9人,其中6人持银卡.
设事件A为“采访该团2人,恰有1人持银卡”,则
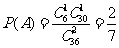
所以采访该团2人,恰有1人持银卡的概率是 . …………………………………6分
. …………………………………6分
(II)设事件B为“采访该团2人,持金卡人数与持银卡人数相等”,可以分为:
事件B1为“采访该团2人,持金卡0人,持银卡0人”,或事件B2为“采访该团2人,持金卡1人,持银卡1人”两种情况,则
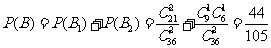
所以采访该团2人,持金卡与持银卡人数相等的概率是 . ……………………12分
. ……………………12分
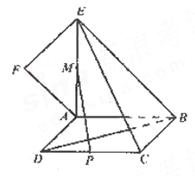 19(本小题满分12分)
19(本小题满分12分)
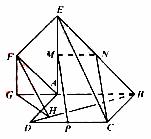
如图,正方形 所在平面与平面四边形
所在平面与平面四边形 所在平面互相垂直,△
所在平面互相垂直,△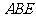 是等腰直角三角形,
是等腰直角三角形,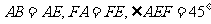
(I)求证: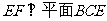 ;
;
(II)设线段 、
、 的中点分别为
的中点分别为 、
、 ,求证:
,求证:  ∥
∥
(III)求二面角 的大小。
的大小。
[解析]解法一:
因为平面ABEF⊥平面ABCD,BC 平面ABCD,BC⊥AB,平面ABEF∩平面ABCD=AB,
平面ABCD,BC⊥AB,平面ABEF∩平面ABCD=AB,
所以BC⊥平面ABEF.
 所以BC⊥EF.
所以BC⊥EF.
因为⊿ABE为等腰直角三角形,AB=AE,
所以∠AEB=45°,
又因为∠AEF=45,
所以∠FEB=90°,即EF⊥BE.
因为BC 平面ABCD, BE
平面ABCD, BE 平面BCE,
平面BCE,
BC∩BE=B
所以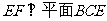
…………………………………………6分
(II)取BE的中点N,连结CN,MN,则MN

 PC
PC
∴ PMNC为平行四边形,所以PM∥CN.
∵ CN在平面BCE内,PM不在平面BCE内,
∴ PM∥平面BCE. …………………………………………8分
(III)由EA⊥AB,平面ABEF⊥平面ABCD,易知EA⊥平面ABCD.
作FG⊥AB,交BA的延长线于G,则FG∥EA.从而FG⊥平面ABCD,
作GH⊥BD于H,连结FH,则由三垂线定理知BD⊥FH.
∴ ∠FHG为二面角F-BD-A的平面角.
∵ FA=FE,∠AEF=45°,
∠AEF=90°, ∠FAG=45°.
设AB=1,则AE=1,AF= ,则
,则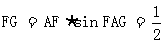
在Rt⊿BGH中, ∠GBH=45°,BG=AB+AG=1+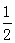 =
= ,
,
 ,
,


在Rt⊿FGH中,  ,
,
∴
二面角 的大小为
的大小为
…………………………………………12分 

解法二: 因 等腰直角三角形,
等腰直角三角形, ,所以
,所以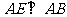
又因为平面 ,所以
,所以 ⊥平面
⊥平面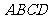 ,所以
,所以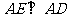
即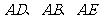 两两垂直;如图建立空间直角坐标系,
两两垂直;如图建立空间直角坐标系,
 (I) 设
(I) 设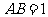 ,则
,则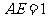 ,
,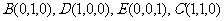
∵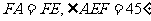 ,∴
,∴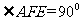 ,
,
从而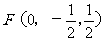


 ,
,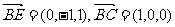
于是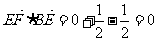 ,
,
∴
 ⊥
⊥ ,
, ⊥
⊥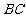
∵
 平面
平面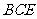 ,
,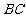
 平面
平面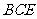 ,
,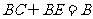
∴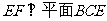
(II) ,从而
,从而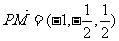
于是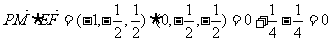
∴ ⊥
⊥ ,又
,又 ⊥平面
⊥平面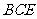 ,直线
,直线 不在平面
不在平面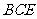 内,
内,
故 ∥平面
∥平面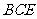
(III)设平面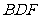 的一个法向量为
的一个法向量为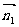 ,并设
,并设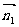 =(
=(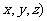
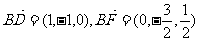
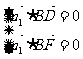 即
即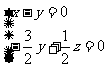
取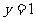 ,则
,则 ,
,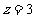 ,从而
,从而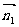 =(1,1,3)
=(1,1,3)
取平面 D的一个法向量为
D的一个法向量为



故二面角 的大小为
的大小为
20(本小题满分12分)
已知函数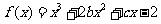 的图象在与
的图象在与 轴交点处的切线方程是
轴交点处的切线方程是 。
。
(I)求函数 的解析式;
的解析式;
(II)设函数 ,若
,若 的极值存在,求实数
的极值存在,求实数 的取值范围以及函数
的取值范围以及函数 取得极值时对应的自变量
取得极值时对应的自变量 的值.
的值.
[解析](I)由已知,切点为(2,0),故有 ,即
,即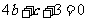 ……①
……①
又 ,由已知
,由已知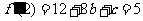 得
得 ……②
……②
联立①②,解得 .
.
所以函数的解析式为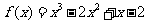 …………………………………4分
…………………………………4分
(II)因为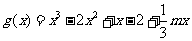
令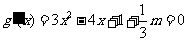
当函数有极值时,则 ,方程
,方程 有实数解,
有实数解, 

由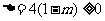 ,得
,得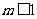 .
.
①当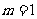 时,
时, 有实数
有实数 ,在
,在 左右两侧均有
左右两侧均有 ,故函数
,故函数 无极值
无极值
②当 时,
时, 有两个实数根
有两个实数根
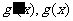 情况如下表:
情况如下表:
 |
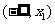 |
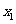 |
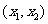 |
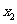 |
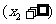 |
 |
+ |
0 |
- |
0 |
+ |
 |
↗ |
极大值 |
↘ |
极小值 |
↗ |
所以在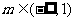 时,函数
时,函数 有极值;
有极值;
当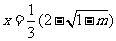 时,
时, 有极大值;当
有极大值;当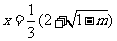 时,
时, 有极小值;
有极小值;
…………………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com