
17.(本小题满分12分)
为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目的个数分别占总数的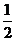 、
、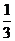 、
、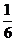 .现有3名工人独立地从中任选一个项目参与建设.求:
.现有3名工人独立地从中任选一个项目参与建设.求:
(I)他们选择的项目所属类别互不相同的概率;
(II)至少有1人选择的项目属于民生工程的概率.
解: 记第 名工人选择的项目属于基础设施工程、民生工程和产业建设工程分别为事件
名工人选择的项目属于基础设施工程、民生工程和产业建设工程分别为事件 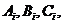 i=1,2,3.由题意知
i=1,2,3.由题意知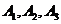 相互独立,
相互独立,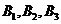 相互独立,
相互独立,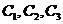
相互独立,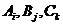 (i,j,k=1,2,3,且i,j,k互不相同)相互独立,
(i,j,k=1,2,3,且i,j,k互不相同)相互独立,
且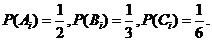
(Ⅰ)他们选择的项目所属类别互不相同的概率
P=
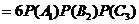
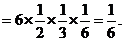
(Ⅱ)至少有1人选择的项目属于民生工程的概率 

P=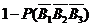
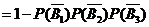
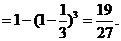
 18.(本小题满分12分)
18.(本小题满分12分)
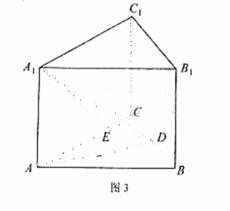
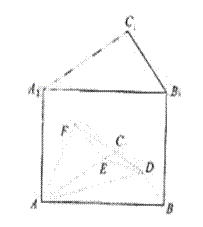
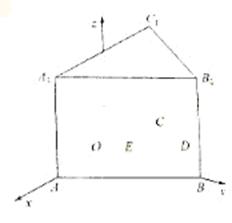
如图3,在正三棱柱 中,
中,
AB=4,
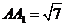 ,点D是BC的中点,
,点D是BC的中点,
点E在AC上,且DE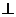
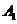 E.
E.
(Ⅰ)证明:平面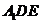
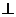 平面
平面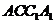 ;
;
(Ⅱ)求直线AD和平面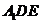 所成角的正弦值。
所成角的正弦值。
解:(Ⅰ)如图所示,由正三棱柱 的性质知
的性质知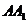
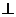 平面
平面 .
.
 又DE
又DE 平面ABC,所以DE
平面ABC,所以DE .而DE
.而DE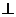
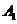 E,
E,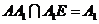 ,
,
所以DE⊥平面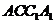 .又DE
.又DE 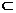 平面
平面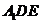 ,
,
故平面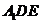 ⊥平面
⊥平面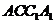 .
.
(Ⅱ)解法 1: 过点A作AF垂直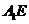 于点
于点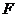 ,
,
连接DF.由(Ⅰ)知,平面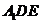 ⊥平面
⊥平面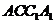 ,
,
所以AF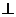 平面
平面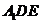 ,故
,故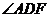 是直线AD和
是直线AD和
平面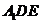 所成的角。
因为DE
所成的角。
因为DE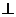
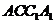 ,
,
所以DE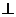 AC.而
AC.而 ABC是边长为4的正三角形,
ABC是边长为4的正三角形,
于是AD=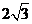 ,AE=4-CE=4-
,AE=4-CE=4-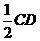 =3.
=3.
又因为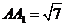 ,所以
,所以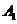 E=
E= 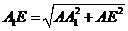
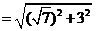 =
4,
=
4, 

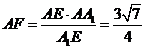 ,
, 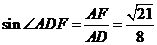 .
.
即直线AD和平面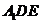 所成角的正弦值为
所成角的正弦值为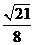 .
.
解法2 : 如图所示,设O是AC的中点,以O为原点建立空间直角坐标系,
则相关各点的坐标分别是A(2,0,0,),
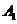 (2,0,
(2,0,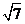 ),
D(-1,
),
D(-1, 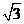 ,0), E(-1,0,0).
,0), E(-1,0,0).
易知 =(-3,
=(-3,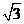 ,-
,-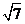 ),
),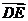 =(0,-
=(0,-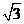 ,0),
,0),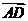 =(-3,
=(-3,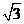 ,0).
,0).
 设
设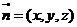 是平面
是平面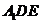 的一个法向量,则
的一个法向量,则
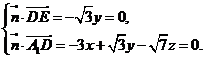
解得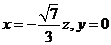 .
.
故可取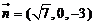 .于是
.于是
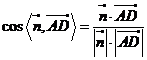 =
=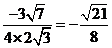 .
. 

由此即知,直线AD和平面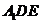 所成角的正弦值为
所成角的正弦值为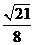 .
.
16.(每小题满分12分)
已知向量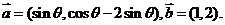
(Ⅰ)若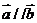 ,求
,求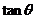 的值;
的值; 

(Ⅱ)若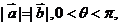 求
求 的值。
的值。
解:(Ⅰ) 因为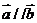 ,所以
,所以
于是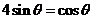 ,故
,故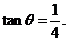
(Ⅱ)由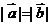 知,
知,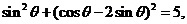
所以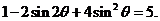
从而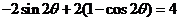 ,即
,即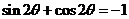 ,
,
于是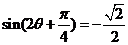 .又由
.又由 知,
知,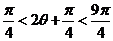 ,
,
所以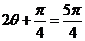 ,或
,或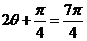 .
.
因此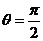 ,或
,或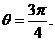
15.如图2,两块斜边长相等的直角三角板拼在一起,若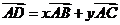 ,则
,则
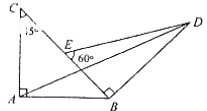
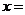
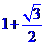 ,
,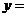
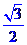 .
.
图2
解:作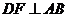 ,设
,设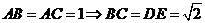 ,
,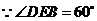 ,
,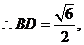
由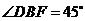 解得
解得 故
故
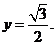
14.在锐角 中,
中,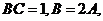 则
则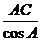 的值等于 2 ,
的值等于 2 ,
 的取值范围为
的取值范围为
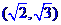 .
. 

解: 设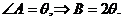 由正弦定理得
由正弦定理得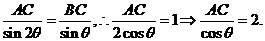
由锐角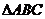 得
得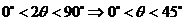 ,
,
又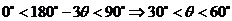 ,故
,故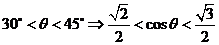 ,
,
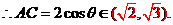
13.过双曲线C: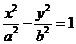
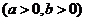 的一个焦点作圆
的一个焦点作圆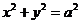 的两条切线,
的两条切线,
切点分别为A,B,若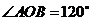 (O是坐标原点),则双曲线线C的离心率为
2
.
(O是坐标原点),则双曲线线C的离心率为
2
.
解: 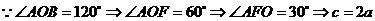 ,
, 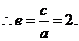
12. 一个总体分为A,B两层,用分层抽样方法从总体中抽取一个容量为10的样本。
已知B层中每个个体被抽到的概率都为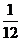 ,则总体中的个体数为 120 .
,则总体中的个体数为 120 .
解: 设总体中的个体数为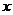 ,则
,则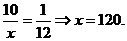
11.在 的展开式中,
的展开式中,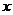 的系数为
6 (用数字作答).
的系数为
6 (用数字作答).
解: 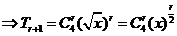 ,故
,故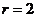 得
得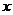 的系数为
的系数为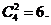
10.若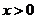 ,则
,则 的最小值为
的最小值为 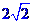 .
. 

解: 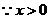
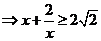 ,当且仅当
,当且仅当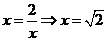 时取等号.
时取等号.
把答案填在答题卡中对应题号后的横线上。
9.某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项
运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为 12 .
解: 设所求人数为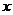 ,则只喜爱乒乓球运动的人数为
,则只喜爱乒乓球运动的人数为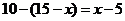 ,
,
故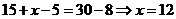 . 注:最好作出韦恩图!
. 注:最好作出韦恩图!
8.设函数 在
在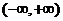 内有定义,对于给定的正数K,定义函数
内有定义,对于给定的正数K,定义函数
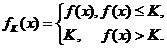
取函数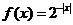 。当
。当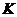 =
=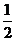 时,函数
时,函数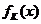 的单调递增区间为[ C ]
的单调递增区间为[ C ]
A .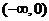 B.
B.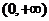 C .
C .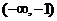 D .
D .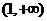
解: 函数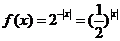 ,作图易知
,作图易知
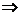
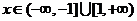 ,
,
故在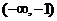 上是单调递增的,选C.
上是单调递增的,选C.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com