
5.2008湖南卷17.(本小题满分12分)
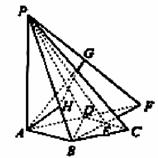
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.
(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求平面PAD和平面PBE所成二面角(锐角)的大小.
解: 解法一(Ⅰ)如图所示,连结BD,由ABCD是菱形且∠BCD=60°知,
 △BCD是等边三角形.因为E是CD的中点,所以BE⊥CD,又AB∥CD,
△BCD是等边三角形.因为E是CD的中点,所以BE⊥CD,又AB∥CD,
所以BE⊥AB.又因为PA⊥平面ABCD, 平面ABCD,所以
平面ABCD,所以
PA⊥BE.而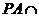 AB=A,因此BE⊥平面PAB.
AB=A,因此BE⊥平面PAB.
又 平面PBE,所以平面PBE⊥平面PAB.
平面PBE,所以平面PBE⊥平面PAB.
(Ⅱ)延长AD、BE相交于点F,连结PF.
过点A作AH⊥PB于H,由(Ⅰ)知
平面PBE⊥平面PAB,所以AH⊥平面PBE.
在Rt△ABF中,因为∠BAF=60°,
所以,AF=2AB=2=AP.
在等腰Rt△PAF中,取PF的中点G,连接AG.
则AG⊥PF.连结HG,由三垂线定理的逆定理得,
PF⊥HG.所以∠AGH是平面PAD和平面PBE所成二面角的平面角(锐角).
在等腰Rt△PAF中,
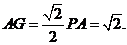
在Rt△PAB中, 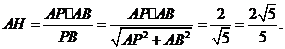
所以,在Rt△AHG中,
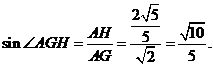
故平面PAD和平面PBE所成二面角(锐角)的大小是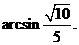
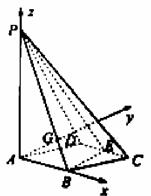
解法二: 如图所示,以A为原点,建立空间直角坐标系.则相关各点的坐标分别是A(0,0,0),B(1,0,0),
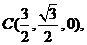
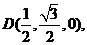 P(0,0,2),
P(0,0,2),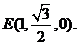
(Ⅰ)因为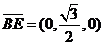 ,
,
平面PAB的一个法向量是 ,
,
所以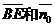 共线.从而BE⊥平面PAB.
共线.从而BE⊥平面PAB.
又因为 平面PBE,
平面PBE,
故平面PBE⊥平面PAB.
(Ⅱ)易知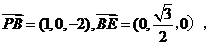
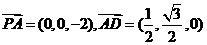
设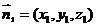 是平面PBE的一个法向量,则由
是平面PBE的一个法向量,则由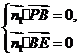 得
得
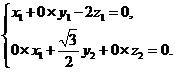 所以
所以
设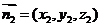 是平面PAD的一个法向量,则由
是平面PAD的一个法向量,则由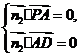 得
得
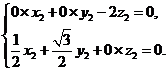 所以
所以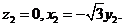 故可取
故可取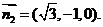
于是,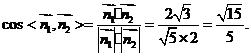
故平面PAD和平面PBE所成二面角(锐角)的大小是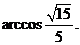
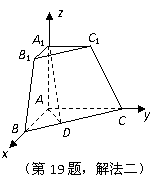
4.2008陕西卷19.(本小题满分12分)
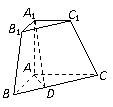 三棱锥被平行于底面
三棱锥被平行于底面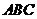 的平面所截得的几何体如图所示,截面为
的平面所截得的几何体如图所示,截面为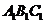 ,
,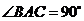 ,
,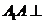 平面
平面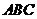 ,
,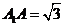 ,
,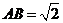 ,
,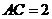 ,
,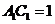 ,
,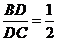 .
.
(Ⅰ)证明:平面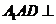 平面
平面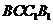 ;
;
(Ⅱ)求二面角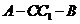 的大小.
的大小.
解法一:(Ⅰ)
 平面
平面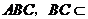 平面
平面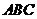 ,
,
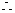
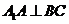 .在
.在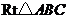 中,
中,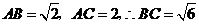 ,
,
 ,
,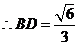 ,又
,又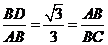 ,
,
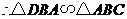 ,
,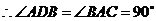 ,即
,即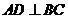 .
.
又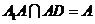 ,
,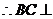 平面
平面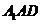 ,
,
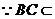 平面
平面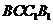 ,
,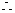 平面
平面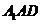
 平面
平面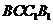 .
.
(Ⅱ)如图,作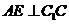 交
交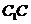 于
于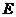 点,连接
点,连接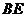 ,
,
由已知得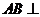 平面
平面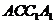 .
.
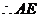 是
是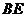 在面
在面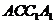 内的射影.
内的射影.
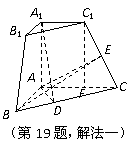 由三垂线定理知
由三垂线定理知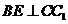 ,
,
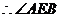 为二面角
为二面角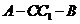 的平面角.
的平面角.
过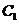 作
作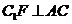 交
交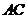 于
于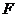 点,
点,
则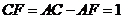 ,
,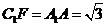 ,
,
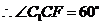 .
.
 在
在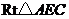 中,
中,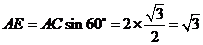 .
.
在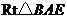 中,
中,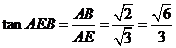 .
.
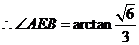 ,
,
即二面角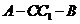 为
为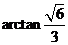 .
.
解法二:(Ⅰ)如图,建立空间直角坐标系,
则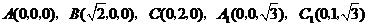 ,
,
 ,
,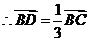 .
.
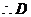 点坐标为
点坐标为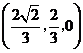 .
.
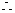
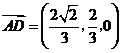 ,
,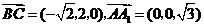 .
.
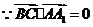 ,
, ,
,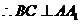 ,
,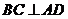 ,又
,又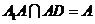 ,
,
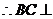 平面
平面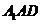 ,又
,又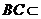 平面
平面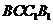 ,
, 平面
平面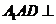 平面
平面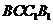 .
.
(Ⅱ)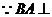 平面
平面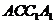 ,取
,取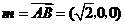 为平面
为平面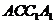 的法向量,
的法向量,
设平面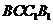 的法向量为
的法向量为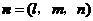 ,则
,则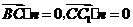 .
.
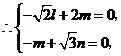
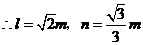 ,
,
如图,可取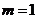 ,则
,则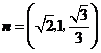 ,
,
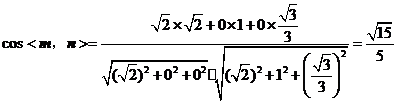 ,
,
即二面角 为
为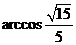 .
.
3.2008辽宁卷19.(本小题满分12分)
如图,在棱长为1的正方体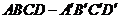 中,AP=BQ=b(0<b<1),截面PQEF∥
中,AP=BQ=b(0<b<1),截面PQEF∥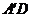 ,截面PQGH∥
,截面PQGH∥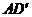 .
.
 (Ⅰ)证明:平面PQEF和平面PQGH互相垂直;
(Ⅰ)证明:平面PQEF和平面PQGH互相垂直;
(Ⅱ)证明:截面PQEF和截面PQGH面积之和是定值,
并求出这个值;
(Ⅲ)若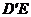 与平面PQEF所成的角为
与平面PQEF所成的角为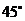 ,求
,求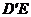 与平
与平
面PQGH所成角的正弦值.
本小题主要考查空间中的线面关系,面面关系,解三角形等基础知识,考查空间想象能力与逻辑思维能力。满分12分.
解法一:
(Ⅰ)证明:在正方体中,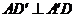 ,
,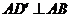 ,又由已知可得
,又由已知可得
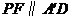 ,
,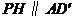 ,
,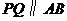 ,
,
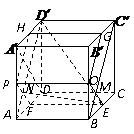 所以
所以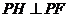 ,
,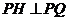 ,
,
所以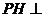 平面
平面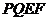 .
.
所以平面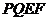 和平面
和平面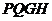 互相垂直.······· 4分
互相垂直.······· 4分
(Ⅱ)证明:由(Ⅰ)知
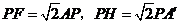 ,又截面PQEF和截面PQGH都是矩形,且PQ=1,所以截面PQEF和截面PQGH面积之和是
,又截面PQEF和截面PQGH都是矩形,且PQ=1,所以截面PQEF和截面PQGH面积之和是
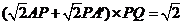 ,是定值.···················· 8分
,是定值.···················· 8分
(III)解:连结BC′交EQ于点M.
因为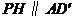 ,
,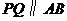 ,
,
所以平面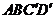 和平面PQGH互相平行,因此
和平面PQGH互相平行,因此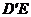 与平面PQGH所成角与
与平面PQGH所成角与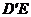 与平面
与平面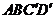 所成角相等.
所成角相等.
与(Ⅰ)同理可证EQ⊥平面PQGH,可知EM⊥平面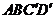 ,因此EM与
,因此EM与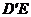 的比值就是所求的正弦值.
的比值就是所求的正弦值.
设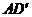 交PF于点N,连结EN,由
交PF于点N,连结EN,由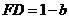 知
知
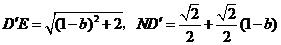 .
.
因为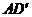 ⊥平面PQEF,又已知
⊥平面PQEF,又已知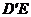 与平面PQEF成
与平面PQEF成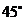 角,
角,
所以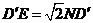 ,即
,即
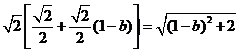 ,
,
解得
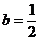 ,可知E为BC中点.
,可知E为BC中点.
所以EM=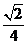 ,又
,又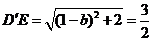 ,
,
故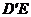 与平面PQCH所成角的正弦值为
与平面PQCH所成角的正弦值为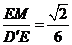 .··············· 12分
.··············· 12分
解法二:
以D为原点,射线DA,DC,DD′分别为x,y,z轴的正半轴建立如图的空间直角坐标系D-xyz由已知得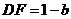 ,故
,故

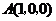 ,
,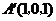 ,
,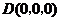 ,
,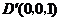 ,
,
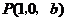 ,
,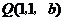 ,
,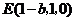 ,
,
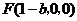 ,
,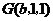 ,
, .
.
(Ⅰ)证明:在所建立的坐标系中,可得
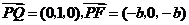 ,
,
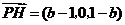 ,
,
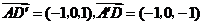 .
.
因为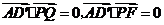 ,所以
,所以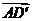 是平面PQEF的法向量.
是平面PQEF的法向量.
因为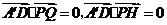 ,所以
,所以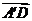 是平面PQGH的法向量.
是平面PQGH的法向量.
因为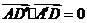 ,所以
,所以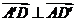 ,
,
所以平面PQEF和平面PQGH互相垂直.····················· 4分
(Ⅱ)证明:因为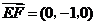 ,所以
,所以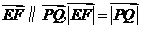 ,又
,又 ,所以PQEF为矩形,同理PQGH为矩形.
,所以PQEF为矩形,同理PQGH为矩形.
在所建立的坐标系中可求得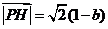 ,
,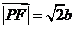 ,
,
所以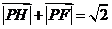 ,又
,又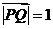 ,
,
所以截面PQEF和截面PQGH面积之和为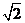 ,是定值.·············· 8分
,是定值.·············· 8分
(Ⅲ)解:由已知得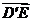 与
与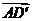 成
成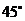 角,又
角,又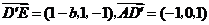 可得
可得

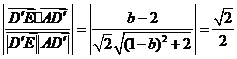 ,
,
 即
即
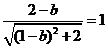 ,解得
,解得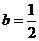 .
.
 所以
所以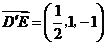 ,又
,又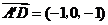 ,所以
,所以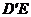 与平面PQGH所成角的正弦值为
与平面PQGH所成角的正弦值为
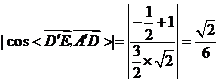 .····················· 12分
.····················· 12分
2.2008江苏卷16.在四面体ABCD 中,CB= CD, AD⊥BD,且E ,F分别是AB,BD 的中点,
求证:(Ⅰ)直线EF ∥面ACD ;
(Ⅱ)面EFC⊥面BCD .
[解析]本小题考查空间直线与平面、平面与平面的位置关系的判定.
(Ⅰ)∵ E,F 分别是AB,BD 的中点,
∴EF 是△ABD 的中位线,∴EF∥AD,
∵EF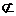 面ACD ,AD
面ACD ,AD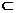 面ACD ,∴直线EF∥面ACD .
面ACD ,∴直线EF∥面ACD .
(Ⅱ)∵ AD⊥BD ,EF∥AD,∴ EF⊥BD.
∵CB=CD, F 是BD的中点,∴CF⊥BD.
又EF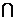 CF=F,∴BD⊥面EFC.∵BD
CF=F,∴BD⊥面EFC.∵BD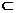 面BCD,∴面EFC⊥面BCD .
面BCD,∴面EFC⊥面BCD .
江西卷.解
:(1)证明:依题设,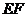 是
是 的中位线,所以
的中位线,所以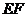 ∥
∥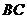 ,
,
 则
则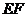 ∥平面
∥平面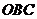 ,所以
,所以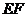 ∥
∥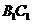 。
。
又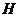 是
是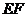 的中点,所以
的中点,所以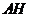 ⊥
⊥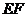 ,则
,则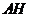 ⊥
⊥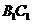 。
。
因为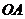 ⊥
⊥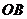 ,
,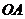 ⊥
⊥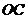 ,
,
所以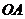 ⊥面
⊥面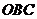 ,则
,则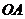 ⊥
⊥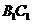 ,
,
因此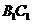 ⊥面
⊥面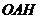 。
。
(2)作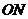 ⊥
⊥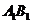 于
于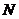 ,连
,连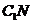 。因为
。因为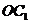 ⊥平面
⊥平面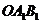 ,
,
根据三垂线定理知,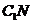 ⊥
⊥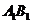 ,
,
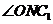 就是二面角
就是二面角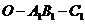 的平面角。
的平面角。
作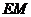 ⊥
⊥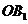 于
于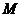 ,则
,则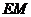 ∥
∥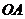 ,则
,则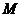 是
是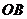 的中点,则
的中点,则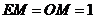 。
。
设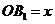 ,由
,由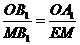 得,
得,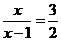 ,解得
,解得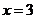 ,
,
在 中,
中,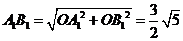 ,则,
,则,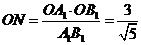 。
。
所以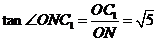 ,故二面角
,故二面角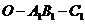 为
为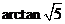 。
。
解法二:(1)以直线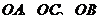 分别为
分别为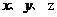 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,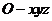 则
则

所以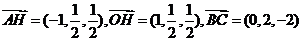
所以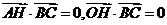
所以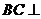 平面
平面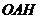
由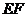 ∥
∥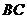 得
得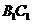 ∥
∥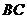 ,故:
,故: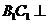 平面
平面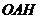
(2)由已知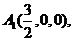 设
设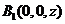
 则
则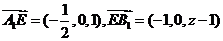
由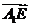 与
与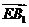 共线得:存在
共线得:存在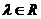 有
有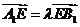 得
得
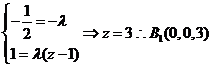
同理: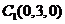
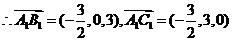
设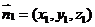 是平面
是平面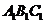 的一个法向量,
的一个法向量,
则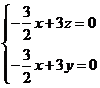 令
令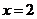 得
得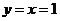
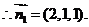
又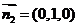 是平面
是平面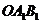 的一个法量
的一个法量
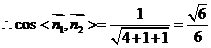
所以二面角的大小为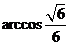
(3)由(2)知,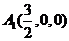 ,
,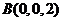 ,平面
,平面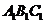 的一个法向量为
的一个法向量为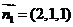 。
。
则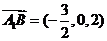 。
。
则点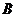 到平面
到平面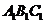 的距离为
的距离为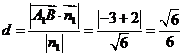
1.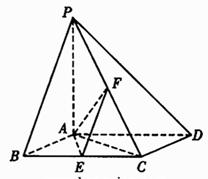 2008山东卷(20)(本小题满分12分)
2008山东卷(20)(本小题满分12分)
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,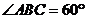 ,E,F分别是BC, PC的中点.
,E,F分别是BC, PC的中点.
(Ⅰ)证明:AE⊥PD;
(Ⅱ)若H为PD上的动点,EH与平面PAD所成最大角的正切值为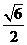 ,求二面角E-AF-C的余弦值.
,求二面角E-AF-C的余弦值.
(Ⅰ)证明:由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.
因为 E为BC的中点,所以AE⊥BC.
又 BC∥AD,因此AE⊥AD.
因为PA⊥平面ABCD,AE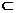 平面ABCD,所以PA⊥AE.
平面ABCD,所以PA⊥AE.
而 PA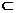 平面PAD,AD
平面PAD,AD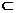 平面PAD 且PA∩AD=A,
平面PAD 且PA∩AD=A,
所以 AE⊥平面PAD,又PD 平面PAD.
平面PAD.
 所以 AE⊥PD.
所以 AE⊥PD.
(Ⅱ)解:设AB=2,H为PD上任意一点,连接AH,EH.
由(Ⅰ)知 AE⊥平面PAD,
则∠EHA为EH与平面PAD所成的角.
在Rt△EAH中,AE=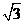 ,
,
所以 当AH最短时,∠EHA最大,
即 当AH⊥PD时,∠EHA最大.
此时 tan∠EHA=
因此 AH= .又AD=2,所以∠ADH=45°,
.又AD=2,所以∠ADH=45°,
所以 PA=2.
解法一:因为 PA⊥平面ABCD,PA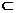 平面PAC,
平面PAC,
所以 平面PAC⊥平面ABCD.
过E作EO⊥AC于O,则EO⊥平面PAC,
过O作OS⊥AF于S,连接ES,则∠ESO为二面角E-AF-C的平面角,
在Rt△AOE中,EO=AE·sin30°=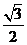 ,AO=AE·cos30°=
,AO=AE·cos30°=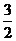 ,
,
又F是PC的中点,在Rt△ASO中,SO=AO·sin45°=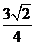 ,
,
又 
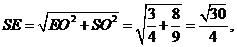
在Rt△ESO中,cos∠ESO=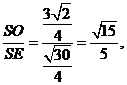
即所求二面角的余弦值为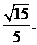
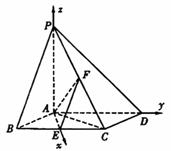 解法二:由(Ⅰ)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,又E、F分别为BC、PC的中点,所以
解法二:由(Ⅰ)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,又E、F分别为BC、PC的中点,所以
E、F分别为BC、PC的中点,所以
A(0,0,0),B(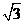 ,-1,0),C(C,1,0),
,-1,0),C(C,1,0),
D(0,2,0),P(0,0,2),E(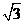 ,0,0),F(
,0,0),F(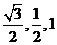 ),
),
所以 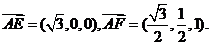
设平面AEF的一法向量为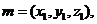
则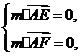 因此
因此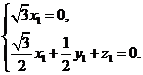
取
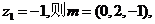
因为 BD⊥AC,BD⊥PA,PA∩AC=A,
所以 BD⊥平面AFC,
故 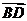 为平面AFC的一法向量.
为平面AFC的一法向量.
又 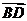 =(-
=(-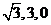 ),
),
所以
cos<m, 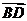 >=
>=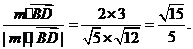
因为 二面角E-AF-C为锐角,
所以所求二面角的余弦值为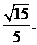

4.利用向量处理距离问题
立体几何中涉及到距离的问题比较多,如两点的距离、点与线的距离、点与面的距离、线与面的距离、两异面直线的距离问题等等,它是数学学习中的一个难点。此部分若用向量来处理,则思路较为简单,方法较为因定。
(1)利用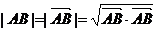 可以求有关距离问题;
可以求有关距离问题;
(2)设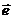 是直线
是直线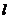 上的一个单位方向向量,线段AB在
上的一个单位方向向量,线段AB在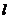 上的投影是
上的投影是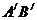 ,则有|
,则有|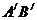 |=
|=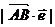 ,由此可求点到线,点到面的距离。
,由此可求点到线,点到面的距离。
3.利用向量处理角度问题
在立体几何中,涉及的角有异面直线所成的角、直线与平面所成的角、二面角等。关于角的计算,均可归结为两个向量的夹角。对于空间向量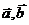 ,有
,有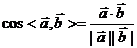 ,利用这一结论,我们可以较方便地处理立体几何中的角的问题。
,利用这一结论,我们可以较方便地处理立体几何中的角的问题。
求异面直线所成的角的关键在于求异面直线上两向量的数量积,而要求两向量的数量积,可以求两向量的坐标,也可以把所求向量用一组基向量表示,两向量的夹角范围是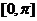 ,而两异面直线所成角的范围是
,而两异面直线所成角的范围是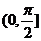 ,应注意加以区分。
,应注意加以区分。
直线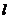 与平面
与平面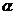 的夹角
的夹角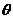 ,是直线
,是直线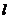 的方向向量
的方向向量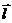 与平面
与平面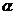 的法向量
的法向量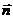 的夹角
的夹角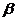 (锐角)的余角,故有:
(锐角)的余角,故有: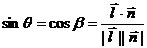 ,
,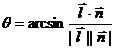 。
。
设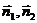 分别是二面角
分别是二面角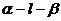 的面
的面 的法向量,则<
的法向量,则<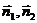 >就是所求二面角的平面角或其补角的大小。
>就是所求二面角的平面角或其补角的大小。
2.利用向量处理垂直问题
空间的线线、线面、面面垂直关系,都可以转化为空间内的两个向量垂直问题来解决。
(1)设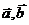 分别为直线
分别为直线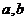 的一个方向向量,那么
的一个方向向量,那么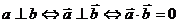 ;
;
(2)设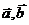 分别为平面
分别为平面 的一个法向量,那么
的一个法向量,那么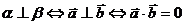 ;
;
(3)设直线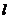 的方向向量为
的方向向量为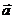 ,平面
,平面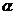 的法向量为
的法向量为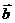 ,那么
,那么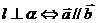 。
。
1.利用向量处理平行问题
空间图形的平行关系包括直线与直线的平行,直线与平面的平行,平面与平面的平行,它们都可以用向量方法来研究。方法如下:
(1)设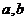 是两条不重合的直线,它们的方向向量分别为
是两条不重合的直线,它们的方向向量分别为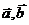 ,那么
,那么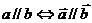 。根据实数与向量积的定义:
。根据实数与向量积的定义: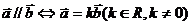 。
。
(2)平面与平面平行可以转化两个平面的法向量平行:设两个不重合的平面 的法向量分别为
的法向量分别为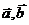 ,那么
,那么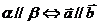 。
。
(3)直线与平面平行可以转化为直线的方向向量与平面与平面的法向量垂直:设直线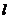 在平面
在平面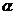 外,
外,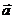 是
是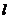 的一个方向向量,
的一个方向向量,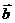 是平面
是平面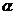 的一个法向量,那么
的一个法向量,那么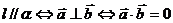 。
。
(4)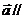 平面
平面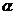
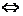 表示以
表示以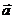 为方向向量的直线与向量
为方向向量的直线与向量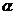 平行或在平面
平行或在平面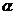 内,因此也可以由共面向量定理证明线面平行问题。
内,因此也可以由共面向量定理证明线面平行问题。
(二)考点预测题
1(2007年宁夏理4).已知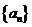 是等差数列,
是等差数列,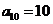 ,其前10项和
,其前10项和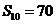 ,则其公差
,则其公差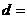 ( )
( )
A.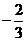 B.
B.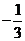 C.
C.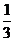 D.
D.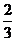
[解析]由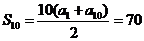 得a1=4, 则a10=a1+9d=4+9d=10,所以
得a1=4, 则a10=a1+9d=4+9d=10,所以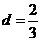 .
.
[答案]D.
2(2008年天津卷20).在数列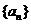 中,
中,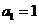 ,
, ,且
,且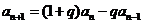 (
(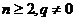 ).
).
(Ⅰ)设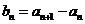 (
(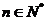 ),证明
),证明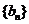 是等比数列;
是等比数列;
(Ⅱ)求数列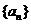 的通项公式;
的通项公式;
(Ⅲ)若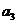 是
是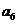 与
与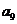 的等差中项,求
的等差中项,求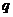 的值,并证明:对任意的
的值,并证明:对任意的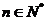 ,
,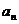 是
是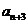 与
与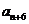 的等差中项.
的等差中项.
[解析](Ⅰ)证明:由题设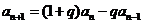 (
(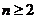 ),得
),得
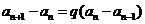 ,即
,即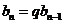 ,
,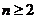 .
.
又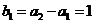 ,
,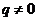 ,所以
,所以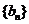 是首项为1,公比为
是首项为1,公比为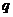 的等比数列.
的等比数列.
(Ⅱ)解法:由(Ⅰ)
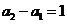 ,
,
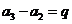 ,
,
……
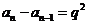 ,(
,(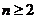 ).
).
将以上各式相加,得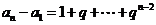 (
(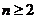 ).
).
所以当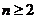 时,
时,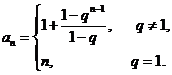
上式对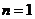 显然成立.
显然成立.
(Ⅲ)解:由(Ⅱ),当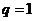 时,显然
时,显然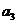 不是
不是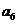 与
与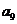 的等差中项,故
的等差中项,故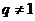 .
.
由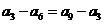 可得
可得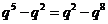 ,由
,由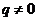 得
得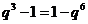 , ①
, ①
整理得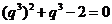 ,解得
,解得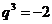 或
或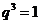 (舍去).于是
(舍去).于是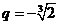 .
.
另一方面,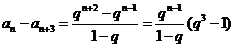 ,
,

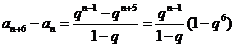 .
.
由①可得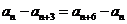 ,
,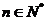 .
.
所以对任意的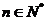 ,
,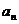 是
是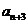 与
与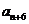 的等差中项.
的等差中项.
3(2008年辽宁卷21).在数列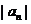 ,
,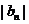 中,a1=2,b1=4,且
中,a1=2,b1=4,且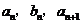 成等差数列,
成等差数列,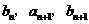 成等比数列(
成等比数列(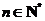 )
)
(Ⅰ)求a2,a3,a4及b2,b3,b4,由此猜测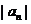 ,
,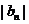 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(Ⅱ)证明: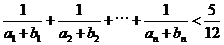 .
.
[解析](Ⅰ)由条件得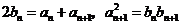
由此可得
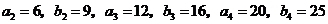 .
.
猜测 .
.
用数学归纳法证明:
①当n=1时,由上可得结论成立.
②假设当n=k时,结论成立,即
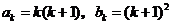 ,
,
那么当n=k+1时,
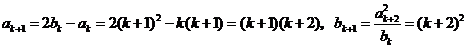 .
.
所以当n=k+1时,结论也成立.
由①②,可知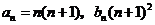 对一切正整数都成立.
对一切正整数都成立.
4(2008-2009学年江苏省盐城市高三数学上学期第一次月考20).已知数列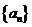 和
和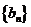 满足
满足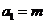 ,
,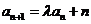 ,
,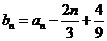 .
.
(Ⅰ) 当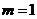 时,求证: 对于任意的实数
时,求证: 对于任意的实数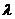 ,
,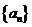 一定不是等差数列;
一定不是等差数列;
(Ⅱ) 当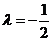 时,试判断
时,试判断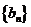 是否为等比数列;
是否为等比数列;
(Ⅲ) 设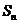 为数列
为数列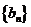 的前
的前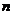 项和,在(Ⅱ)的条件下,是否存在实数
项和,在(Ⅱ)的条件下,是否存在实数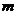 ,使得对任意的正
,使得对任意的正
整数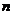 ,都有
,都有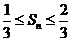 ?若存在,请求出
?若存在,请求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
[解析](Ⅰ)当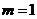 时,
时,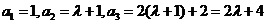
假设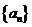 是等差数列,由
是等差数列,由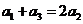 得
得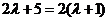 ,即5=2,矛盾.
,即5=2,矛盾.
故对于任意的实数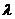 ,
,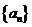 一定不是等差数列.
一定不是等差数列.
(Ⅱ)当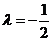 时,
时,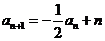 .而
.而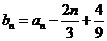 ,所以
,所以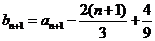
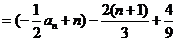 =
=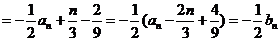 .
.
又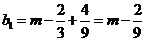 .
.
故当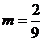 时,
时, 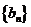 不是等比数列.
不是等比数列.
当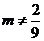 时,
时, 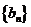 是以
是以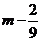 为首项,
为首项,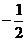 为公比的等比数列.
为公比的等比数列.
(Ⅲ)由(Ⅱ)知,当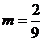 时,
时,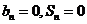 ,不合要求.
,不合要求.
所以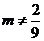 ,于是
,于是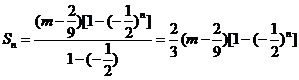 ,要使
,要使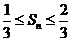 成立,
成立,
则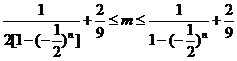 .
.
令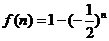 ,当n正奇数时,
,当n正奇数时,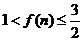 ;当n正偶数时,
;当n正偶数时,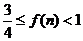 .
.
故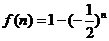 的最大值为
的最大值为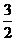 ,最小值为
,最小值为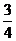 .
.
欲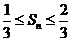 对任意的正整数n都成立,则
对任意的正整数n都成立,则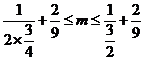 ,即
,即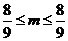 ,所以
,所以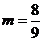 .
.
综上所述,存在唯一的实数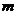 =
=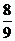 ,使得对任意的正整数
,使得对任意的正整数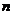 ,都有
,都有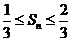 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com