
2、设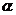 、
、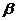 、
、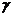 为平面,给出下列条件:(1)
为平面,给出下列条件:(1)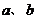 为异面直线,
为异面直线,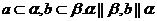 ,(2)
,(2)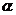 内距离为
内距离为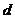 的平行直线在
的平行直线在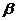 内射影仍为两条距离为
内射影仍为两条距离为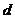 的平行线;(3)
的平行线;(3)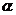 内不共线的三点到
内不共线的三点到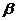 的距离相等;(4)
的距离相等;(4)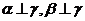 ;其中能使
;其中能使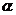 ||
||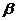 成立的条件的个数为( )
成立的条件的个数为( )
A、1 B、2 C、3 D、4
1、若有平面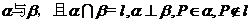 则下列命题中的假命为( )
则下列命题中的假命为( )
A、过点P且垂直于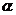 的直线平行于
的直线平行于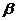 ; B、过点P且垂直于
; B、过点P且垂直于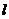 的平面垂直于
的平面垂直于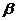 ;
;
C、过点P且垂直于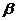 的直线在
的直线在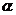 内; D、过点P且垂直于
内; D、过点P且垂直于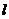 的直线在
的直线在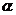 内;
内;
例1.正方体ABCD-A1B1C1D1中.
(1)求证:平面A1BD∥平面B1D1C;
(2)若E、F分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD.
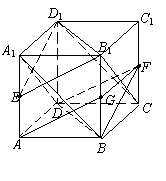 证明:(1)由B1B∥DD1,得四边形BB1D1D是平行四边形,
证明:(1)由B1B∥DD1,得四边形BB1D1D是平行四边形,
∴B1D1∥BD,
又BD Ë平面B1D1C,B1D1 平面B1D1C,
平面B1D1C,
∴BD∥平面B1D1C.
同理A1D∥平面B1D1C.
而A1D∩BD=D,
∴平面A1BD∥平面B1CD.
(2)由BD∥B1D1,得BD∥平面EB1D1.
取BB1中点G,∴AE∥B1G.
从而得B1E∥AG,同理GF∥AD.
∴AG∥DF.
∴B1E∥DF.
∴DF∥平面EB1D1.
∴平面EB1D1∥平面FBD.
说明 要证“面面平面”只要证“线面平面”,要证“线面平行”,只要证“线线平面”,故问题最终转化为证线与线的平行.
 例2.在四面体
例2.在四面体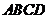 中,
中,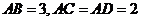 ,且
,且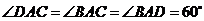 ,
,
求证:平面 ⊥平面
⊥平面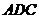
例3.如图,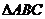 为正三角形,
为正三角形,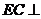 平面
平面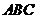 ,
,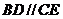 ,且
,且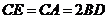 ,
,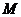 是
是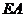 的中点,
的中点,
 求证:(1)
求证:(1)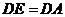 ;(2)平面
;(2)平面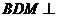 平面
平面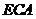 ;(3)平面
;(3)平面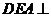 平面
平面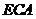 。
。
例4三棱锥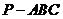 中,
中,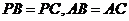 ,点
,点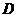 为
为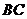 中点,
中点,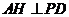 于
于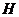 点,连
点,连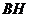 ,求证:平面
,求证:平面 平面
平面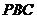
6.已知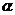 ,
,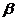 是两个平面,直线
是两个平面,直线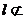
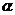 ,
,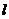
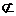
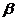 ,设(1)
,设(1)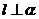 ,(2)
,(2)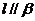 ,(3)
,(3)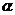
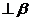 ,若以其中两个作为条件,另一个作为结论,则正确命题的个数是
( )
,若以其中两个作为条件,另一个作为结论,则正确命题的个数是
( )
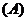 0
0 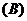 1
1 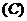 2
2 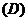 3
3
5.若三个平面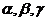 ,之间有
,之间有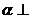
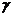 ,
,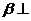
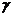 ,则
,则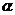 与
与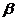 ( )
( )
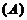 垂直
垂直 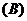 平行
平行 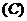 相交
相交 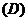 以上三种可能都有
以上三种可能都有
4.平面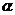 ⊥平面
⊥平面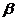 ,
,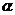
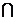
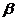 =
=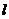 ,点
,点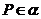 ,点
,点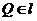 ,那么
,那么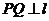 是
是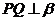 的( )
的( )
 充分但不必要条件
充分但不必要条件  必要但不充分条件
必要但不充分条件  充要条件
充要条件 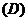 既不充分也不必要条件
既不充分也不必要条件
3.已知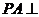 正方形
正方形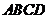 所在的平面,垂足为
所在的平面,垂足为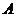 ,连结
,连结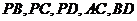 ,则互相垂直的平面有
( )
,则互相垂直的平面有
( )
 5对
5对  6对
6对  7对
7对  8对
8对
2.空间四边形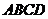 的两条对角线
的两条对角线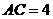 ,
,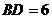 ,则平行于两对角线的截面四边形的周长的取值范围是
.答案:(8,12)
,则平行于两对角线的截面四边形的周长的取值范围是
.答案:(8,12)
1.已知平面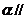 平面
平面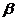 ,
,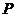 是
是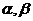 外一点,过点
外一点,过点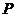 的直线
的直线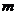 与
与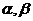 分别交于点
分别交于点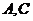 ,过点
,过点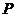 的直线
的直线 与
与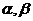 分别交于点
分别交于点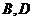 ,且
,且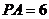 ,
,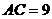 ,
,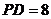 ,则
,则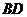 的长为(
的长为( 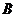 )
)
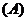
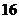
 或
或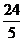
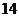
7.两平面垂直的性质定理:(面面垂直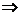 线面垂直)
线面垂直)
若两个平面互相垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面。
二基本训练:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com