
4.若函数 是函数
是函数 的反函数,且
的反函数,且 ,则
,则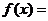
A.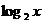 B.
B. C.
C. D.2
D.2
[答案]A
[解析]函数 的反函数是
的反函数是 ,又
,又 ,即
,即 ,
,
所以, ,故
,故 ,选A.
,选A.
3.已知平面向量a= ,b=
,b= , 则向量
, 则向量
A平行于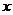 轴
B.平行于第一、三象限的角平分线
轴
B.平行于第一、三象限的角平分线
C.平行于 轴
D.平行于第二、四象限的角平分线
轴
D.平行于第二、四象限的角平分线
[答案]
[解析]
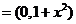 ,由
,由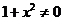 及向量的性质可知,C正确.
及向量的性质可知,C正确.
2.下列n的取值中,使 =1(i是虚数单位)的是
=1(i是虚数单位)的是
A.n=2 B .n=3 C .n=4 D .n=5
[答案]C
[解析]因为 ,故选C.
,故选C.
1.已知全集U=R,则正确表示集合M= {-1,0,1} 和N= { x |x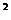 +x=0} 关系的韦恩(Venn)图是
+x=0} 关系的韦恩(Venn)图是

[答案]B
[解析]由N= { x |x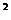 +x=0}
+x=0}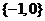 得
得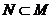 ,选B.
,选B.
21.(本小题满分14分) 

已知二次函数
 的导函数的图像与直线
的导函数的图像与直线 平行,且
平行,且 在
在 处取得极小值
处取得极小值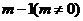 。设函数
。设函数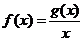 。
。 

(1)若曲线 上的点
上的点 到点
到点 的距离的最小值为
的距离的最小值为 ,求
,求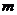 的值;
的值;
(2) 如何取值时,函数
如何取值时,函数 存在零点,并求出零点。
存在零点,并求出零点。
20.(本小题满分14分)
已知点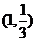 是函数
是函数 的图像上一点。等比数列
的图像上一点。等比数列 的前n项和为
的前n项和为 。数列
。数列 的首项为c,且前n项和
的首项为c,且前n项和 满足
满足
(1)求数列 和
和 的通项公式;
的通项公式; 

(2)若数列 的前
的前 项和为
项和为 ,问满足
,问满足 >
> 的最小正整数
的最小正整数 是多少?
是多少?
19.(本小题满分14分)
已知椭圆G的中心在坐标原点,长轴在x轴上,离心率为 ,两个焦点分别为
,两个焦点分别为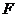
 和
和 ,椭圆G上一点到
,椭圆G上一点到 和
和 的距离之和为12。圆
的距离之和为12。圆 :
: 的圆心为点
的圆心为点 。
。
(1)求椭圆G的方程;
(2)求
 面积;
面积;
(3)问是否存在圆 包围椭圆G?请说明理由。
包围椭圆G?请说明理由。 

18.(本小题满分13分)
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7。

(1)根据茎叶图判断哪个班的平均身高较高; 

(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。 

17.(本小题满分13分)
某高速公路收费站入口处的安全标识墩如图4所示。墩的上半部分是正四棱锥 ,下半部分是长方体
,下半部分是长方体 。图5、图6分别是该标识墩的正(主)视图和俯视图。
。图5、图6分别是该标识墩的正(主)视图和俯视图。
(1)请画出该安全标识墩的侧(左)视图; 

(2)求该安全标识墩的体积;
(3)证明:直线 平面
平面 .
.

16.(本小题满分12分)
已知向量 与
与 互相垂直,其中
互相垂直,其中 .
.
(1) 求 和
和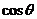 的值;
的值;
(2) 若 ,求
,求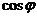 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com