
3.探究 F
(1)从不同的角度和层面发掘文本的深层意蕴
(2)探讨文本反映的人生价值和时代精神
(3)探究文本中的终点和难点,提出自己的见解
2.鉴赏评价 D
(1)评价文本的主要观点和基本倾向
(2)评价文本产生的社会价值和影响
(3)对文本的某种特色作深度的思考和判断
20.已知二次函数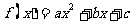 .
.
(1)若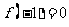 ,试判断函数
,试判断函数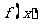 零点个数;
零点个数;
(2)若对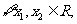 且
且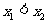 ,
,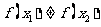 ,试证明
,试证明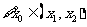 ,使
,使
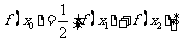 成立;
成立;
(3)是否存在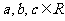 ,使
,使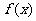 同时满足以下条件①对
同时满足以下条件①对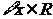 ,
,
 ,且
,且 ;②对
;②对 ,都有
,都有
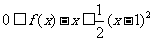 .若存在,求出
.若存在,求出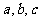 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
江苏省海头高级中学2011届高三数学综合练习(2)
19.公差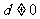 的等差数列
的等差数列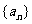 的前
的前 项和为
项和为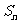 ,已知
,已知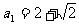 ,
,
(1)求数列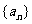 的通项公式
的通项公式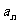 及其前
及其前 项和
项和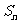 ;
;
(2)记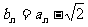 ,若自然数
,若自然数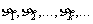 满足
满足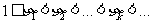 ,并且
,并且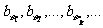 成等比数列,其中
成等比数列,其中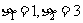 ,求
,求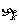 (用
(用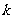 表示);
表示);
(3)记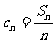 ,试问:在数列
,试问:在数列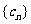 中是否存在三项
中是否存在三项
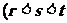 ,
,
 恰好成等比数列?若存在,求出此三项;若不存在,请说明理由.
恰好成等比数列?若存在,求出此三项;若不存在,请说明理由.
18.经市场调查,某商场的一种商品在过去的一个月内(以30天计)销售价格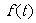 (元)与时间
(元)与时间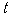 (天)的函数关系近似满足
(天)的函数关系近似满足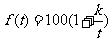 (
(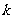 为正常数),日销售量
为正常数),日销售量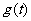 (件)与时间
(件)与时间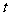 (天)的函数关系近似满足
(天)的函数关系近似满足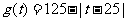 ,且第25天的销售金额为13000元.
,且第25天的销售金额为13000元.
(1)求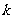 的值;
的值;
(2)试写出该商品的日销售金额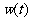 关于时间
关于时间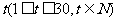 的函数关系式;
的函数关系式;
(3)该商品的日销售金额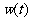 的最小值是多少?.
的最小值是多少?.
17.已知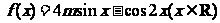 .
.
(1)若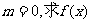 的单调递增区间;
的单调递增区间;
(2)若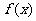 的最大值为3,求实数m的值.
的最大值为3,求实数m的值.
16.在平面直角坐标系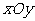 中,点
中,点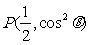 在角
在角 的终边上,点
的终边上,点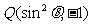 在角
在角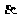 的终边上,且
的终边上,且 .
.
(1)求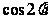 的值;
的值;
(2)求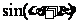 .
.
15.已知数列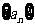 为等差数列,且
为等差数列,且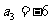 ,
,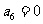 .
.
(1)求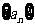 的通项公式;
的通项公式;
(2)若等比数列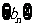 满足
满足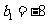 ,
,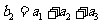 ,求
,求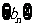 的前n项和公式.
的前n项和公式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com