
8.在样本的频率分布直方图中,共有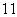 个小长方形,若中间一个小长方形的面积等于其他
个小长方形,若中间一个小长方形的面积等于其他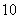 个小长方形的面积之和的
个小长方形的面积之和的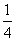 ,且样本容量为
,且样本容量为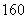 ,则中间一组的频数为 32 .
,则中间一组的频数为 32 .
7.一个总体中有100个个体,随机编号0,1,2,…,99,依编号顺序平均分成10个小
组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为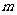 ,那么在第
,那么在第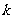 组中抽取的号码个位数字与
组中抽取的号码个位数字与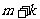 的个位数字相同,若
的个位数字相同,若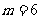 ,则在第7组中抽取的号码是 63 .
,则在第7组中抽取的号码是 63 .
6.某校有老师200人,男学生1200人,女学生1000人.现用分层抽样的方法从所有师生中抽取一个容量为 的样本;已知从女学生中抽取的人数为80人,则
的样本;已知从女学生中抽取的人数为80人,则
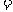
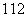 .
.
5.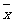 是
是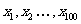 的平均数,
的平均数,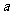 是
是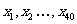 的平均数,
的平均数,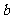 是
是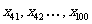 的平均数,则
的平均数,则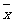 ,
,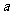 ,
,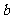 之间的关系为
之间的关系为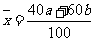 .
.
3.设有 个样本
个样本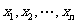 ,其标准差为
,其标准差为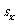 ,另有
,另有 个样本
个样本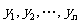 ,且
,且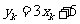
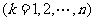 ,其标准差为
,其标准差为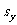 ,则下列关系正确的是 ( B )
,则下列关系正确的是 ( B )
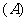
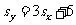
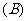
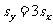
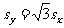
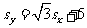
2.已知样本方差由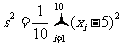 ,求得,则
,求得,则
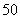 .
.
1.某公司甲、乙、丙、丁四个地区分别有150 个、120个、180个、150个销售点.公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中有20个特大型销售点,要从中抽取7个调查其收入和售后服务等情况,记这项调查为②.则完成①、②这两项调查宜采用的抽样方法依次是 ( B )
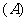 分层抽样法,系统抽样法
分层抽样法,系统抽样法 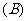 分层抽样法,简单随机抽样法
分层抽样法,简单随机抽样法
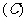 系统抽样法,分层抽样法
系统抽样法,分层抽样法 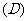 简单随机抽样法,分层抽样法
简单随机抽样法,分层抽样法
[例1] (2004年湖南,5)某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点.公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为②.则完成①、②这两项调查宜采用的抽样方法依次是
A.分层抽样法,系统抽样法 B.分层抽样法,简单随机抽样法
C.系统抽样法,分层抽样法 D.简单随机抽样法,分层抽样法
剖析:此题为抽样方法的选取问题.当总体中个体较多时宜采用系统抽样;当总体中的个体差异较大时,宜采用分层抽样;当总体中个体较少时,宜采用随机抽样.
依据题意,第①项调查应采用分层抽样法、第②项调查应采用简单随机抽样法.故选B.
答案:B
评述:采用什么样的抽样方法要依据研究的总体中的个体情况来定.
[例2] (2004年福建,15)一个总体中有100个个体,随机编号为0,1,2,…,99,依编号顺序平均分成10个小组,组号依次为1,2,3,…,10.现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k小组中抽取的号码个位数字与m+k的个位数字相同.若m=6,则在第7组中抽取的号码是___________.
剖析:此问题总体中个体的个数较多,因此采用系统抽样.按题目中要求的规则抽取即可.
∵m=6,k=7,m+k=13,∴在第7小组中抽取的号码是63.
答案:63
评述:当总体中个体个数较多而差异又不大时可采用系统抽样.采用系统抽样在每小组内抽取时应按规则进行.
[例3] 把容量为100的某个样本数据分为10组,并填写频率分布表,若前七组的累积频率为0.79,而剩下三组的频数成公比大于2的整数等比数列,则剩下三组中频数最高的一组的频数为___________.
剖析:已知前七组的累积频率为0.79,而要研究后三组的问题,因此应先求出后三组的频率之和为1-0.79=0.21,进而求出后三组的共有频数,或者先求前七组共有频数后,再计算后三组的共有频数.
由已知知前七组的累积频数为0.79×100=79,故后三组共有的频数为21,依题意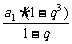 =21,a1(1+q+q2)=21.∴a1=1,q=4.∴后三组频数最高的一组的频数为16.
=21,a1(1+q+q2)=21.∴a1=1,q=4.∴后三组频数最高的一组的频数为16.
答案:16
评述:此题剖析只按第二种思路给出了解答,你能按第一种思路来解吗?
[例4] 对某电子元件进行寿命追踪调查,情况如下:
|
寿命(h) |
100-200 |
200-300 |
300-400 |
400-500 |
500-600 |
|
个 数 |
20 |
30 |
80 |
40 |
30 |
(1)列出频率分布表;
(2)画出频率分布直方图和累积频率分布图;
(3)估计电子元件寿命在100-400 h以内的概率;
(4)估计电子元件寿命在400 h以上的概率.
剖析:通过本题可掌握总体分布估计的各种方法和步骤.
解:(1)频率分布表如下:
|
寿命(h) |
频 数 |
频 率 |
累积频率 |
|
100-200 |
20 |
0.10 |
0.10 |
|
200-300 |
30 |
0.15 |
0.25 |
|
300-400 |
80 |
0.40 |
0.65 |
|
400-500 |
40 |
0.20 |
0.85 |
|
500-600 |
30 |
0.15 |
1 |
|
合 计 |
200 |
1 |
|
(2)频率分布直方图如下:
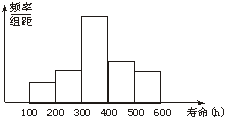
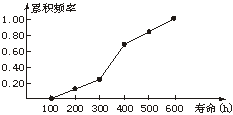
(3)由累积频率分布图可以看出,寿命在100-400 h内的电子元件出现的频率为0.65,所以我们估计电子元件寿命在100-400 h内的概率为0.65.
(4)由频率分布表可知,寿命在400 h以上的电子元件出现的频率为0.20+0.15=0.35,故我们估计电子元件寿命在400 h以上的概率为0.35.
评述:画频率分布条形图、直方图时要注意纵、横坐标轴的意义.
[例5] 某批零件共160个,其中,一级品48个,二级品64个,三级品32个,等外品16个.从中抽取一个容量为20的样本.请说明分别用简单随机抽样、系统抽样和分层抽样法抽取时总体中的每个个体被取到的概率均相同.
[例6]一个容量为100的样本,数据的分组和各组的一些相关信息如下:
|
分 组 |
频 数 |
频 率 |
累积频率 |
|
[12,15) |
6 |
|
|
|
[15,18) |
|
0.08 |
|
|
[18,21) |
|
|
0.30 |
|
[21,24) |
21 |
|
|
|
[24,27) |
|
|
0.69 |
|
[27,30) |
16 |
|
|
|
[30,33] |
|
0.10 |
|
|
[33,36) |
|
|
1.00 |
|
合 计 |
100 |
1.00 |
|
(1)完成上表;
(2)画出频率分布直方图和累积频率分布图;
(3)根据累积频率分布图,总体中小于22的样本数据大约占多大的百分比?
〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓
5.某班学生在一次数学考试中成绩分布如下表:
|
分数段 |
[0,80) |
[80,90) |
[90,100) |
||
|
人数 |
2 |
|
6 |
||
|
分数段 |
[100,110) |
[110,120 |
[120,130) |
||
|
人数 |
8 |
12 |
6 |
||
|
分数段 |
[130,140) |
[140,150) |
|
||
|
人数 |
4 |
2 |
|
那么分数在[100,110)中的频率和分数不满110分的累积频率分别是______________、_______(精确到0.01).
解析:由频率计算方法知:总人数=45.
分数在[100,110)中的频率为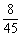 =0.178≈0.18.
=0.178≈0.18.
分数不满110分的累积频率为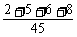 =
=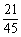 ≈0.47.
≈0.47.
答案:0.18 0.47
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com